“Mplus SEM Example 5.12”的版本间的差异
来自OBHRM百科
Lichaoping(讨论 | 贡献) |
Lichaoping(讨论 | 贡献) |
||
| (未显示同一用户的4个中间版本) | |||
| 第1行: | 第1行: | ||
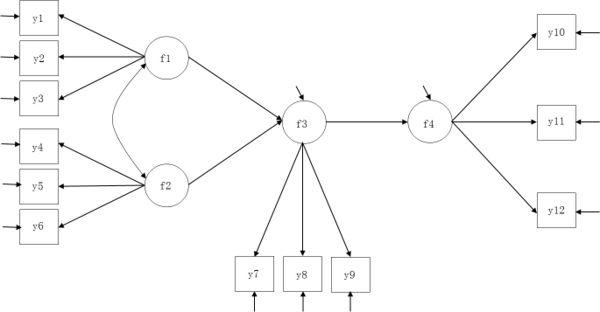
| + | ==示意图== | ||
| + | [[文件:mplus0512.jpg | center |600px]] | ||
| + | |||
| + | ==代码与注释== | ||
| + | <pre>TITLE:this is an example of a SEM with ! 这是标题,总共两行内容,第一行 | ||
| + | continuous factor indicator and an ! 第二行 | ||
| + | indirect effect for factors ! 第三行,想要多少行,就写多少行 | ||
| + | DATA:FILE IS ex5.12.dat; !读数据文件,文件名要正确,文件路径与对应的分析程序在同一目录下;或标明绝对路径,比如:c:\mplus\ex5.12.dat。 | ||
| + | VARIABLE:NAMES ARE y1-y12; ! 读取数据,该数据文件中包括12个变量的数据,变量名称可以自己定。 | ||
| + | MODEL: f1 BY y1-y3 ! 定义第1个因素,该因素的测量指标有:y1,y2,y3。如果上面为item1-item12,则修改为item1-item3。 | ||
| + | f2 BY y4-y6; ! 定义第2个因素,该因素的测量指标有:y4,y5,y6。 | ||
| + | f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。 | ||
| + | f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。 | ||
| + | f4 ON f3; ! 因子f3变量预测因子f4 | ||
| + | f3 ON f1 f2; ! 因子f1 f2两个变量预测因子f3 | ||
| + | MODEL INDIRECT: ! 模型间接效应 | ||
| + | f4 IND f3 f1; ! f4为因变量,f1为自变量,f3为中介变量,即指定自变量f1通过中介变量f3对因变量f4的间接效应 | ||
| + | OUTPUT:STANDARDIZED; ! 报告标准化之后的结果,这是增加的命令语句。</pre> | ||
| + | |||
==结果== | ==结果== | ||
| + | <pre>INPUT INSTRUCTIONS !@ 输入的命令语句,会全部显示,下面几行就是输入的命令语句 | ||
| + | |||
| + | TITLE:this is an example of a SEM with ! 这是标题,总共两行内容,第一行 | ||
| + | continuous factor indicator and an ! 第二行 | ||
| + | indirect effect for factors ! 第三行,想要多少行,就写多少行 | ||
| + | DATA:FILE IS ex5.12.dat; ! 读数据文件,文件名要正确,文件路径与对应的分析程序在同一目录下;或标明绝对路径,比如:c:\mplus\ex5.12.dat。 | ||
| + | VARIABLE:NAMES ARE y1-y12; ! 读取数据,该数据文件中包括12个变量的数据,变量名称可以自己定。比如,可以是y1-y12,也可以是item1-item12。 | ||
| + | MODEL: f1 BY y1-y3; ! 定义第1个因素,该因素的测量指标有:y1,y2,y3。如果上面为item1-item12,则修改为item1-item3。 | ||
| + | f2 BY y4-y6; ! 定义第2个因素,该因素的测量指标有:y4,y5,y6。 | ||
| + | f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。 | ||
| + | f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。 | ||
| + | f4 ON f3; ! 因子f3变量预测因子f4 | ||
| + | f3 ON f1 f2; ! 因子f1 f2两个变量预测因子f3 | ||
| + | MODEL INDIRECT: ! 模型间接效应 | ||
| + | f4 IND f3 f1; ! f4为因变量,f1为自变量,f3为中介变量,即指定自变量f1通过中介变量f3对因变量f4的间接效应 | ||
| + | OUTPUT:STANDARDIZED; ! 报告标准化之后的结果,这是增加的命令语句。 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | INPUT READING TERMINATED NORMALLY !输入指令读取正常终止,如果是非正常终止,就需要检查数据或命令语句。 | ||
| + | |||
| + | |||
| + | |||
| + | TITLE:this is an example of a SEM with ! 这是标题,总共两行内容,第一行 | ||
| + | continuous factor indicator and an ! 第二行 | ||
| + | indirect effect for factors ! 第三行,想要多少行,就写多少行 | ||
| + | |||
| + | SUMMARY OF ANALYSIS !@分析总体情况 | ||
| + | |||
| + | Number of groups 1 !@ 1组数据,也就是样本没有分组 | ||
| + | Number of observations 500 !@ 样本量500 | ||
| + | |||
| + | Number of dependent variables 12 !@ (因)变量12个 | ||
| + | Number of independent variables 0 !@ (自)变量0个 | ||
| + | Number of continuous latent variables 4 !@ 潜变量4个 | ||
| + | |||
| + | Observed dependent variables !@ 观测(因)变量 | ||
| + | |||
| + | Continuous | ||
| + | Y1 Y2 Y3 Y4 Y5 Y6 !@ 观测(因)变量为连续变量 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10 Y11 Y12 | ||
| + | Y7 Y8 Y9 Y10 Y11 Y12 | ||
| + | |||
| + | Continuous latent variables !@ 潜变量 F1 F2 F3 F4 | ||
| + | F1 F2 F3 F4 | ||
| + | |||
| + | |||
| + | Estimator ML !@ 估计方法:最大似然法 | ||
| + | Information matrix OBSERVED !@ 信息矩阵:观测数据 | ||
| + | Maximum number of iterations 1000 !@ 最大迭代次数1000次 | ||
| + | Convergence criterion 0.500D-04 !@ 聚合标准(或翻译为收敛标准) | ||
| + | Maximum number of steepest descent iterations 20 !@ 迭代下降最大数:20 | ||
| + | |||
| + | Input data file(s) !@ 输入文件:ex5.12.dat | ||
| + | ex5.11.dat | ||
| + | |||
| + | Input data format FREE !@ 输入文件格式:自由格式,这是Mplus的默认格式 | ||
| + | |||
| + | |||
| + | |||
| + | THE MODEL ESTIMATION TERMINATED NORMALLY !@ 模型估计正常终止,如果是非正常终止,就需要检查数据或命令语句 | ||
| + | |||
| + | |||
| + | |||
| + | MODEL FIT INFORMATION !@ 模型拟合指数 | ||
| + | |||
| + | Number of Free Parameters 40 !@ 自由参数的个数:40个 | ||
| + | |||
| + | Loglikelihood !@ 似然函数值的自然对数 | ||
| + | |||
| + | H0 Value -9646.960 | ||
| + | H1 Value -9620.108 | ||
| + | |||
| + | Information Criteria !@ 信息标准 | ||
| + | |||
| + | Akaike (AIC) 19373.920 !@ AIC | ||
| + | Bayesian (BIC) 19542.505 !@ BIC | ||
| + | Sample-Size Adjusted BIC 19415.542 !@ 考虑样本量调整后的BIC值 | ||
| + | (n* = (n + 2) / 24) | ||
| + | |||
| + | Chi-Square Test of Model Fit !@ 卡方检验的结果 | ||
| + | |||
| + | Value 53.704 !@ 卡方值 | ||
| + | Degrees of Freedom 50 !@ 自由度 | ||
| + | P-Value 0.3344 !@ 显著性 | ||
| + | |||
| + | RMSEA (Root Mean Square Error Of Approximation) !@ RMSEA的结果 | ||
| + | |||
| + | Estimate 0.012 !@ RMSEA的值 | ||
| + | 90 Percent C.I. 0.000 0.032 !@ RMSEA的90%置信区间 | ||
| + | Probability RMSEA <= .05 1.000 | ||
| + | |||
| + | CFI/TLI !@ CFI/TFI的结果 | ||
| + | |||
| + | CFI 0.997 !@ CFI的结果 | ||
| + | TLI 0.997 !@ TLI的结果 | ||
| + | |||
| + | Chi-Square Test of Model Fit for the Baseline Model !@ 基准模型(基线模型)的卡方检验结果 | ||
| + | |||
| + | Value 1524.403 !@ 卡方值 | ||
| + | Degrees of Freedom 66 !@ 自由度 | ||
| + | P-Value 0.0000 !@ 显著性 | ||
| + | |||
| + | SRMR (Standardized Root Mean Square Residual) !@ SRMR的结果 | ||
| + | |||
| + | Value 0.027 | ||
| + | |||
| + | |||
| + | |||
| + | MODEL RESULTS !@ 模型结果,非标准化的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 BY | ||
| + | Y1 1.000 0.000 999.000 999.000 !@ Y1的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | Y2 1.183 0.104 11.376 0.000 !@ Y2的非标准化因子负荷 | ||
| + | Y3 0.938 0.087 10.818 0.000 !@ Y3的非标准化因子负荷 | ||
| + | |||
| + | F2 BY | ||
| + | Y4 1.000 0.000 999.000 999.000 !@ Y4的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | Y5 0.870 0.085 10.202 0.000 !@ Y2的非标准化因子负荷 | ||
| + | Y6 0.891 0.092 9.735 0.000 !@ Y3的非标准化因子负荷 | ||
| + | |||
| + | F3 BY | ||
| + | Y7 1.000 0.000 999.000 999.000 !@ Y7的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | Y8 0.872 0.059 14.699 0.000 !@ Y8的非标准化因子负荷 | ||
| + | Y9 0.882 0.060 14.611 0.000 !@ Y9的非标准化因子负荷 | ||
| + | |||
| + | F4 BY | ||
| + | Y10 1.000 0.000 999.000 999.000 !@ Y10的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | Y11 0.826 0.094 8.812 0.000 !@ Y11的非标准化因子负荷 | ||
| + | Y12 0.682 0.089 7.696 0.000 !@ Y12的非标准化因子负荷 | ||
| + | |||
| + | F4 ON | ||
| + | F3 0.473 0.057 8.306 0.000 !@ F3到F4的系数 | ||
| + | |||
| + | F3 ON | ||
| + | F1 0.563 0.070 8.027 0.000 !@ F1到F3的系数 | ||
| + | F2 0.790 0.086 9.228 0.000 !@ F1到F3的系数 | ||
| + | |||
| + | F2 WITH | ||
| + | F1 -0.030 0.055 -0.545 0.586 !@ F1 F2之间的相关系数 | ||
| + | |||
| + | Intercepts !@ 截距,潜变量为0时,观察变量的值 | ||
| + | Y1 0.011 0.062 0.183 0.855 !@ Y1的截距 | ||
| + | Y2 0.047 0.064 0.738 0.460 !@ Y2的截距 | ||
| + | Y3 0.005 0.062 0.078 0.938 !@ Y3的截距 | ||
| + | Y4 0.104 0.064 1.627 0.104 !@ Y4的截距 | ||
| + | Y5 0.078 0.057 1.361 0.173 !@ Y5的截距 | ||
| + | Y6 0.074 0.059 1.241 0.215 !@ Y6的截距 | ||
| + | Y7 0.051 0.068 0.754 0.451 !@ Y7的截距 | ||
| + | Y8 0.063 0.063 1.000 0.317 !@ Y8的截距 | ||
| + | Y9 0.078 0.063 1.248 0.212 !@ Y9的截距 | ||
| + | Y10 -0.008 0.064 -0.128 0.898 !@ Y10的截距 | ||
| + | Y11 0.039 0.055 0.716 0.474 !@ Y11的截距 | ||
| + | Y12 0.031 0.054 0.563 0.574 !@ Y12的截距 | ||
| + | |||
| + | Variances !@ 因子方差 | ||
| + | F1 0.884 0.122 7.234 0.000 !@ F1的方差,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | F2 0.888 0.130 6.830 0.000 !@ F2的方差,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | |||
| + | Residual Variances !@ 残差,潜变量未能解释的方差 | ||
| + | Y1 1.033 0.094 11.034 0.000 !@ Y1的残差 | ||
| + | Y2 0.795 0.101 7.862 0.000 !@ Y2的残差 | ||
| + | Y3 1.137 0.092 12.389 0.000 !@ Y3的残差 | ||
| + | Y4 1.151 0.104 11.039 0.000 !@ Y4的残差 | ||
| + | Y5 0.950 0.083 11.468 0.000 !@ Y5的残差 | ||
| + | Y6 1.056 0.091 11.670 0.000 !@ Y6的残差 | ||
| + | Y7 0.954 0.089 10.762 0.000 !@ Y7的残差 | ||
| + | Y8 0.945 0.079 11.980 0.000 !@ Y8的残差 | ||
| + | Y9 0.896 0.077 11.581 0.000 !@ Y9的残差 | ||
| + | Y10 1.202 0.118 10.193 0.000 !@ Y10的残差 | ||
| + | Y11 0.916 0.085 10.777 0.000 !@ Y11的残差 | ||
| + | Y12 1.071 0.083 12.834 0.000 !@ Y12的残差 | ||
| + | F3 0.550 0.092 5.961 0.000 !@ F3的残差 | ||
| + | F4 0.555 0.102 5.422 0.000 !@ F4的残差 | ||
| + | |||
| + | |||
| + | STANDARDIZED MODEL RESULTS !@ 模型结果,标准化的结果 | ||
| + | |||
| + | |||
| + | STDYX Standardization !@ 观测变量、潜变量均标准化后的结果,也就是全部标准化后的结果。一般报告这个结果。 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 BY | ||
| + | Y1 0.679 0.035 19.246 0.000 !@ Y1的标准化因子负荷 | ||
| + | Y2 0.780 0.033 23.806 0.000 !@ Y2的标准化因子负荷 | ||
| + | Y3 0.637 0.035 18.004 0.000 !@ Y3的标准化因子负荷 | ||
| + | |||
| + | F2 BY | ||
| + | Y4 0.660 0.038 17.593 0.000 !@ Y4的标准化因子负荷 | ||
| + | Y5 0.644 0.038 17.002 0.000 !@ Y5的标准化因子负荷 | ||
| + | Y6 0.633 0.038 16.496 0.000 !@ Y6的标准化因子负荷 | ||
| + | |||
| + | F3 BY | ||
| + | Y7 0.766 0.026 29.462 0.000 !@ Y7的标准化因子负荷 | ||
| + | Y8 0.723 0.028 25.845 0.000 !@ Y8的标准化因子负荷 | ||
| + | Y9 0.736 0.028 26.747 0.000 !@ Y9的标准化因子负荷 | ||
| + | |||
| + | F4 BY | ||
| + | Y10 0.646 0.043 15.098 0.000 !@ Y10的标准化因子负荷 | ||
| + | Y11 0.625 0.043 14.546 0.000 !@ Y11的标准化因子负荷 | ||
| + | Y12 0.521 0.046 11.444 0.000 !@ Y12的标准化因子负荷 | ||
| + | |||
| + | F4 ON | ||
| + | F3 0.595 0.049 12.145 0.000 !@ F3到F4的系数 | ||
| + | |||
| + | F3 ON | ||
| + | F1 0.454 0.048 9.535 0.000 !@ F1到F3的系数 | ||
| + | F2 0.639 0.044 14.485 0.000 !@ F2到F3的系数 | ||
| + | |||
| + | F2 WITH | ||
| + | F1 -0.034 0.062 -0.545 0.586 !@ F1 F2之间的相关系数 | ||
| + | |||
| + | Intercepts !@ 截距,潜变量为0时,观察变量的值 | ||
| + | Y1 0.008 0.045 0.183 0.855 !@ Y1的截距 | ||
| + | Y2 0.033 0.045 0.738 0.460 !@ Y2的截距 | ||
| + | Y3 0.003 0.045 0.078 0.938 !@ Y3的截距 | ||
| + | Y4 0.073 0.045 1.625 0.104 !@ Y4的截距 | ||
| + | Y5 0.061 0.045 1.360 0.174 !@ Y5的截距 | ||
| + | Y6 0.055 0.045 1.240 0.215 !@ Y6的截距 | ||
| + | Y7 0.034 0.045 0.754 0.451 !@ Y7的截距 | ||
| + | Y8 0.045 0.045 0.999 0.318 !@ Y8的截距 | ||
| + | Y9 0.056 0.045 1.247 0.212 !@ Y9的截距 | ||
| + | Y10 -0.006 0.045 -0.128 0.898 !@ Y10的截距 | ||
| + | Y11 0.032 0.045 0.716 0.474 !@ Y11的截距 | ||
| + | Y12 0.025 0.045 0.563 0.574 !@ Y12的截距 | ||
| + | |||
| + | Variances !@ 因子方差 | ||
| + | F1 1.000 0.000 999.000 999.000 !@ F1的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | F2 1.000 0.000 999.000 999.000 !@ F2的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | |||
| + | Residual Variances !@ 残差,潜变量未能解释的方差 | ||
| + | Y1 0.539 0.048 11.249 0.000 !@ Y1的残差 | ||
| + | Y2 0.392 0.051 7.660 0.000 !@ Y2的残差 | ||
| + | Y3 0.594 0.045 13.174 0.000 !@ Y3的残差 | ||
| + | Y4 0.565 0.050 11.403 0.000 !@ Y4的残差 | ||
| + | Y5 0.586 0.049 12.024 0.000 !@ Y5的残差 | ||
| + | Y6 0.600 0.049 12.361 0.000 !@ Y6的残差 | ||
| + | Y7 0.413 0.040 10.352 0.000 !@ Y7的残差 | ||
| + | Y8 0.478 0.040 11.832 0.000 !@ Y8的残差 | ||
| + | Y9 0.459 0.040 11.333 0.000 !@ Y9的残差 | ||
| + | Y10 0.583 0.055 10.565 0.000 !@ Y10的残差 | ||
| + | Y11 0.610 0.054 11.374 0.000 !@ Y11的残差 | ||
| + | Y12 0.728 0.047 15.351 0.000 !@ Y12的残差 | ||
| + | F3 0.405 0.056 7.206 0.000 !@ F3的残差 | ||
| + | F4 0.646 0.058 11.088 0.000 !@ F4的残差 | ||
| + | |||
| + | |||
| + | STDY Standardization !@ 观测变量标准化后的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 BY | ||
| + | Y1 0.679 0.035 19.246 0.000 !@ Y1的标准化因子负荷 | ||
| + | Y2 0.780 0.033 23.806 0.000 !@ Y2的标准化因子负荷 | ||
| + | Y3 0.637 0.035 18.004 0.000 !@ Y3的标准化因子负荷 | ||
| + | |||
| + | F2 BY | ||
| + | Y4 0.660 0.038 17.593 0.000 !@ Y4的标准化因子负荷 | ||
| + | Y5 0.644 0.038 17.002 0.000 !@ Y5的标准化因子负荷 | ||
| + | Y6 0.633 0.038 16.496 0.000 !@ Y6的标准化因子负荷 | ||
| + | |||
| + | F3 BY | ||
| + | Y7 0.766 0.026 29.462 0.000 !@ Y7的标准化因子负荷 | ||
| + | Y8 0.723 0.028 25.845 0.000 !@ Y8的标准化因子负荷 | ||
| + | Y9 0.736 0.028 26.747 0.000 !@ Y9的标准化因子负荷 | ||
| + | |||
| + | F4 BY | ||
| + | Y10 0.646 0.043 15.098 0.000 !@ Y10的标准化因子负荷 | ||
| + | Y11 0.625 0.043 14.546 0.000 !@ Y11的标准化因子负荷 | ||
| + | Y12 0.521 0.046 11.444 0.000 !@ Y12的标准化因子负荷 | ||
| + | |||
| + | F4 ON | ||
| + | F3 0.595 0.049 12.145 0.000 !@ F3到F4的系数 | ||
| + | |||
| + | F3 ON | ||
| + | F1 0.454 0.048 9.535 0.000 !@ F1到F3的系数 | ||
| + | F2 0.639 0.044 14.485 0.000 !@ F2到F3的系数 | ||
| + | |||
| + | F2 WITH | ||
| + | F1 -0.034 0.062 -0.545 0.586 !@ F1 F2之间的相关系数 | ||
| + | |||
| + | Intercepts !@ 截距,潜变量为0时,观察变量的值 | ||
| + | Y1 0.008 0.045 0.183 0.855 !@ Y1的截距 | ||
| + | Y2 0.033 0.045 0.738 0.460 !@ Y2的截距 | ||
| + | Y3 0.003 0.045 0.078 0.938 !@ Y3的截距 | ||
| + | Y4 0.073 0.045 1.625 0.104 !@ Y4的截距 | ||
| + | Y5 0.061 0.045 1.360 0.174 !@ Y5的截距 | ||
| + | Y6 0.055 0.045 1.240 0.215 !@ Y6的截距 | ||
| + | Y7 0.034 0.045 0.754 0.451 !@ Y7的截距 | ||
| + | Y8 0.045 0.045 0.999 0.318 !@ Y8的截距 | ||
| + | Y9 0.056 0.045 1.247 0.212 !@ Y9的截距 | ||
| + | Y10 -0.006 0.045 -0.128 0.898 !@ Y10的截距 | ||
| + | Y11 0.032 0.045 0.716 0.474 !@ Y11的截距 | ||
| + | Y12 0.025 0.045 0.563 0.574 !@ Y12的截距 | ||
| + | |||
| + | Variances !@ 因子方差 | ||
| + | F1 1.000 0.000 999.000 999.000 !@ F1的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | F2 1.000 0.000 999.000 999.000 !@ F2的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | |||
| + | Residual Variances !@ 残差,潜变量未能解释的方差 | ||
| + | Y1 0.539 0.048 11.249 0.000 !@ Y1的残差 | ||
| + | Y2 0.392 0.051 7.660 0.000 !@ Y2的残差 | ||
| + | Y3 0.594 0.045 13.174 0.000 !@ Y3的残差 | ||
| + | Y4 0.565 0.050 11.403 0.000 !@ Y4的残差 | ||
| + | Y5 0.586 0.049 12.024 0.000 !@ Y5的残差 | ||
| + | Y6 0.600 0.049 12.361 0.000 !@ Y6的残差 | ||
| + | Y7 0.413 0.040 10.352 0.000 !@ Y7的残差 | ||
| + | Y8 0.478 0.040 11.832 0.000 !@ Y8的残差 | ||
| + | Y9 0.459 0.040 11.333 0.000 !@ Y9的残差 | ||
| + | Y10 0.583 0.055 10.565 0.000 !@ Y10的残差 | ||
| + | Y11 0.610 0.054 11.374 0.000 !@ Y11的残差 | ||
| + | Y12 0.728 0.047 15.351 0.000 !@ Y12的残差 | ||
| + | F3 0.405 0.056 7.206 0.000 !@ F3的残差 | ||
| + | F4 0.646 0.058 11.088 0.000 !@ F4的残差 | ||
| + | |||
| + | |||
| + | STD Standardization !@ 潜变量标准化后的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 BY | ||
| + | Y1 0.940 0.065 14.467 0.000 !@ Y1的标准化因子负荷 | ||
| + | Y2 1.112 0.066 16.789 0.000 !@ Y2的标准化因子负荷 | ||
| + | Y3 0.881 0.064 13.771 0.000 !@ Y3的标准化因子负荷 | ||
| + | |||
| + | F2 BY | ||
| + | Y4 0.942 0.069 13.659 0.000 !@ Y4的标准化因子负荷 | ||
| + | Y5 0.820 0.062 13.326 0.000 !@ Y5的标准化因子负荷 | ||
| + | Y6 0.840 0.064 13.047 0.000 !@ Y6的标准化因子负荷 | ||
| + | |||
| + | F3 BY | ||
| + | Y7 1.165 0.064 18.327 0.000 !@ Y7的标准化因子负荷 | ||
| + | Y8 1.016 0.060 17.018 0.000 !@ Y8的标准化因子负荷 | ||
| + | Y9 1.028 0.059 17.368 0.000 !@ Y9的标准化因子负荷 | ||
| + | |||
| + | F4 BY | ||
| + | Y10 0.927 0.075 12.352 0.000 !@ Y10的标准化因子负荷 | ||
| + | Y11 0.765 0.064 11.999 0.000 !@ Y11的标准化因子负荷 | ||
| + | Y12 0.632 0.063 9.954 0.000 !@ Y12的标准化因子负荷 | ||
| + | |||
| + | F4 ON | ||
| + | F3 0.595 0.049 12.145 0.000 !@ F3到F4的系数 | ||
| + | |||
| + | F3 ON | ||
| + | F1 0.454 0.048 9.535 0.000 !@ F1到F3的系数 | ||
| + | F2 0.639 0.044 14.485 0.000 !@ F2到F3的系数 | ||
| + | |||
| + | F2 WITH | ||
| + | F1 -0.034 0.062 -0.545 0.586 !@ F1 F2之间的相关系数 | ||
| + | |||
| + | Intercepts !@ 截距,潜变量为0时,观察变量的值 | ||
| + | Y1 0.011 0.062 0.183 0.855 !@ Y1的截距 | ||
| + | Y2 0.047 0.064 0.738 0.460 !@ Y2的截距 | ||
| + | Y3 0.005 0.062 0.078 0.938 !@ Y3的截距 | ||
| + | Y4 0.104 0.064 1.627 0.104 !@ Y4的截距 | ||
| + | Y5 0.078 0.057 1.361 0.173 !@ Y5的截距 | ||
| + | Y6 0.074 0.059 1.241 0.215 !@ Y6的截距 | ||
| + | Y7 0.051 0.068 0.754 0.451 !@ Y7的截距 | ||
| + | Y8 0.063 0.063 1.000 0.317 !@ Y8的截距 | ||
| + | Y9 0.078 0.063 1.248 0.212 !@ Y9的截距 | ||
| + | Y10 -0.008 0.064 -0.128 0.898 !@ Y10的截距 | ||
| + | Y11 0.039 0.055 0.716 0.474 !@ Y11的截距 | ||
| + | Y12 0.031 0.054 0.563 0.574 !@ Y12的截距 | ||
| + | |||
| + | Variances !@ 因子方差 | ||
| + | F1 1.000 0.000 999.000 999.000 !@ F1的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | F2 1.000 0.000 999.000 999.000 !@ F1的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | |||
| + | Residual Variances !@ 残差,潜变量未能解释的方差 | ||
| + | Y1 1.033 0.094 11.034 0.000 !@ Y1的残差 | ||
| + | Y2 0.795 0.101 7.862 0.000 !@ Y2的残差 | ||
| + | Y3 1.137 0.092 12.389 0.000 !@ Y3的残差 | ||
| + | Y4 1.151 0.104 11.039 0.000 !@ Y4的残差 | ||
| + | Y5 0.950 0.083 11.468 0.000 !@ Y5的残差 | ||
| + | Y6 1.056 0.091 11.670 0.000 !@ Y6的残差 | ||
| + | Y7 0.954 0.089 10.762 0.000 !@ Y7的残差 | ||
| + | Y8 0.945 0.079 11.980 0.000 !@ Y8的残差 | ||
| + | Y9 0.896 0.077 11.581 0.000 !@ Y9的残差 | ||
| + | Y10 1.202 0.118 10.193 0.000 !@ Y10的残差 | ||
| + | Y11 0.916 0.085 10.777 0.000 !@ Y11的残差 | ||
| + | Y12 1.071 0.083 12.834 0.000 !@ Y12的残差 | ||
| + | F3 0.405 0.056 7.206 0.000 !@ F3的残差 | ||
| + | F4 0.646 0.058 11.088 0.000 !@ F4的残差 | ||
| + | |||
| + | |||
| + | R-SQUARE !@ R的平方,观测变量、潜变量被因子解释的百分比 | ||
| + | |||
| + | Observed Two-Tailed | ||
| + | Variable Estimate S.E. Est./S.E. P-Value !@ 观测变量 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Y1 0.461 0.048 9.623 0.000 !@ Y1被F1解释的百分比 | ||
| + | Y2 0.608 0.051 11.903 0.000 !@ Y2被F1解释的百分比 | ||
| + | Y3 0.406 0.045 9.002 0.000 !@ Y3被F1解释的百分比 | ||
| + | Y4 0.435 0.050 8.797 0.000 !@ Y4被F2解释的百分比 | ||
| + | Y5 0.414 0.049 8.501 0.000 !@ Y5被F2解释的百分比 | ||
| + | Y6 0.400 0.049 8.248 0.000 !@ Y6被F2解释的百分比 | ||
| + | Y7 0.587 0.040 14.731 0.000 !@ Y7被F3解释的百分比 | ||
| + | Y8 0.522 0.040 12.923 0.000 !@ Y8被F3解释的百分比 | ||
| + | Y9 0.541 0.040 13.373 0.000 !@ Y9被F3解释的百分比 | ||
| + | Y10 0.417 0.055 7.549 0.000 !@ Y10被F4解释的百分比 | ||
| + | Y11 0.390 0.054 7.273 0.000 !@ Y11被F4解释的百分比 | ||
| + | Y12 0.272 0.047 5.722 0.000 !@ Y12被F4解释的百分比 | ||
| + | |||
| + | Latent Two-Tailed | ||
| + | Variable Estimate S.E. Est./S.E. P-Value !@ 潜变量 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F3 0.595 0.056 10.581 0.000 !@ F3被F1、F2解释的百分比 | ||
| + | F4 0.354 0.058 6.073 0.000 !@ F4被F3解释的百分比 | ||
| + | |||
| + | |||
| + | QUALITY OF NUMERICAL RESULTS | ||
| + | |||
| + | Condition Number for the Information Matrix 0.448E-01 !@ 信息矩阵的条件数 | ||
| + | (ratio of smallest to largest eigenvalue) | ||
| + | |||
| + | |||
| + | TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS !@总效应,总间接效应,具体间接效应和直接效应 | ||
| + | |||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Effects from F1 to F4 !@F1到F4的影响 | ||
| + | |||
| + | Indirect 0.266 0.043 6.144 0.000 | ||
| + | |||
| + | |||
| + | STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS !@标准化总效应,总间接效应,具体间接效应和直接效应 | ||
| + | |||
| + | |||
| + | STDYX Standardization !@ 观测变量、潜变量均标准化后的结果,也就是全部标准化后的结果。一般报告这个结果。 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Effects from F1 to F4 !@F1到F4的影响 | ||
| + | |||
| + | Indirect 0.270 0.036 7.478 0.000 | ||
| + | |||
| + | |||
| + | STDY Standardization !@ 观测变量标准化后的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Effects from F1 to F4 !@F1到F4的影响 | ||
| + | |||
| + | Indirect 0.270 0.036 7.478 0.000 | ||
| + | |||
| + | |||
| + | STD Standardization !@ 潜变量标准化后的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | |||
| + | Effects from F1 to F4 !@F1到F4的影响 | ||
| + | |||
| + | Indirect 0.270 0.036 7.478 0.000 | ||
| + | |||
| + | |||
| + | |||
| + | DIAGRAM INFORMATION !@ 图形信息 | ||
| + | |||
| + | Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram. !@ 在Diagram菜单下显示图形信息 | ||
| + | If running Mplus from the Mplus Diagrammer, the diagram opens automatically. !@ 如果是从Mplus Diagrammer运行Mplus,会自动显示图形信息 | ||
| + | |||
| + | |||
| + | Diagram output !图形输出路径 | ||
| + | c:\program files\mplus\mplus examples\user's guide examples\ex5.12.dgm | ||
| + | |||
| + | Beginning Time: 12:30:10 !@ 命令语句(程序)开始运行时间 | ||
| + | Ending Time: 12:30:12 !@ 命令语句(程序)结束运行时间 | ||
| + | Elapsed Time: 00:00:02 !@ 程序运行花费时间</pre> | ||
2017年6月17日 (六) 12:36的最新版本
示意图
代码与注释
TITLE:this is an example of a SEM with ! 这是标题,总共两行内容,第一行
continuous factor indicator and an ! 第二行
indirect effect for factors ! 第三行,想要多少行,就写多少行
DATA:FILE IS ex5.12.dat; !读数据文件,文件名要正确,文件路径与对应的分析程序在同一目录下;或标明绝对路径,比如:c:\mplus\ex5.12.dat。
VARIABLE:NAMES ARE y1-y12; ! 读取数据,该数据文件中包括12个变量的数据,变量名称可以自己定。
MODEL: f1 BY y1-y3 ! 定义第1个因素,该因素的测量指标有:y1,y2,y3。如果上面为item1-item12,则修改为item1-item3。
f2 BY y4-y6; ! 定义第2个因素,该因素的测量指标有:y4,y5,y6。
f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。
f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。
f4 ON f3; ! 因子f3变量预测因子f4
f3 ON f1 f2; ! 因子f1 f2两个变量预测因子f3
MODEL INDIRECT: ! 模型间接效应
f4 IND f3 f1; ! f4为因变量,f1为自变量,f3为中介变量,即指定自变量f1通过中介变量f3对因变量f4的间接效应
OUTPUT:STANDARDIZED; ! 报告标准化之后的结果,这是增加的命令语句。
结果
INPUT INSTRUCTIONS !@ 输入的命令语句,会全部显示,下面几行就是输入的命令语句
TITLE:this is an example of a SEM with ! 这是标题,总共两行内容,第一行
continuous factor indicator and an ! 第二行
indirect effect for factors ! 第三行,想要多少行,就写多少行
DATA:FILE IS ex5.12.dat; ! 读数据文件,文件名要正确,文件路径与对应的分析程序在同一目录下;或标明绝对路径,比如:c:\mplus\ex5.12.dat。
VARIABLE:NAMES ARE y1-y12; ! 读取数据,该数据文件中包括12个变量的数据,变量名称可以自己定。比如,可以是y1-y12,也可以是item1-item12。
MODEL: f1 BY y1-y3; ! 定义第1个因素,该因素的测量指标有:y1,y2,y3。如果上面为item1-item12,则修改为item1-item3。
f2 BY y4-y6; ! 定义第2个因素,该因素的测量指标有:y4,y5,y6。
f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。
f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。
f4 ON f3; ! 因子f3变量预测因子f4
f3 ON f1 f2; ! 因子f1 f2两个变量预测因子f3
MODEL INDIRECT: ! 模型间接效应
f4 IND f3 f1; ! f4为因变量,f1为自变量,f3为中介变量,即指定自变量f1通过中介变量f3对因变量f4的间接效应
OUTPUT:STANDARDIZED; ! 报告标准化之后的结果,这是增加的命令语句。
INPUT READING TERMINATED NORMALLY !输入指令读取正常终止,如果是非正常终止,就需要检查数据或命令语句。
TITLE:this is an example of a SEM with ! 这是标题,总共两行内容,第一行
continuous factor indicator and an ! 第二行
indirect effect for factors ! 第三行,想要多少行,就写多少行
SUMMARY OF ANALYSIS !@分析总体情况
Number of groups 1 !@ 1组数据,也就是样本没有分组
Number of observations 500 !@ 样本量500
Number of dependent variables 12 !@ (因)变量12个
Number of independent variables 0 !@ (自)变量0个
Number of continuous latent variables 4 !@ 潜变量4个
Observed dependent variables !@ 观测(因)变量
Continuous
Y1 Y2 Y3 Y4 Y5 Y6 !@ 观测(因)变量为连续变量 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10 Y11 Y12
Y7 Y8 Y9 Y10 Y11 Y12
Continuous latent variables !@ 潜变量 F1 F2 F3 F4
F1 F2 F3 F4
Estimator ML !@ 估计方法:最大似然法
Information matrix OBSERVED !@ 信息矩阵:观测数据
Maximum number of iterations 1000 !@ 最大迭代次数1000次
Convergence criterion 0.500D-04 !@ 聚合标准(或翻译为收敛标准)
Maximum number of steepest descent iterations 20 !@ 迭代下降最大数:20
Input data file(s) !@ 输入文件:ex5.12.dat
ex5.11.dat
Input data format FREE !@ 输入文件格式:自由格式,这是Mplus的默认格式
THE MODEL ESTIMATION TERMINATED NORMALLY !@ 模型估计正常终止,如果是非正常终止,就需要检查数据或命令语句
MODEL FIT INFORMATION !@ 模型拟合指数
Number of Free Parameters 40 !@ 自由参数的个数:40个
Loglikelihood !@ 似然函数值的自然对数
H0 Value -9646.960
H1 Value -9620.108
Information Criteria !@ 信息标准
Akaike (AIC) 19373.920 !@ AIC
Bayesian (BIC) 19542.505 !@ BIC
Sample-Size Adjusted BIC 19415.542 !@ 考虑样本量调整后的BIC值
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit !@ 卡方检验的结果
Value 53.704 !@ 卡方值
Degrees of Freedom 50 !@ 自由度
P-Value 0.3344 !@ 显著性
RMSEA (Root Mean Square Error Of Approximation) !@ RMSEA的结果
Estimate 0.012 !@ RMSEA的值
90 Percent C.I. 0.000 0.032 !@ RMSEA的90%置信区间
Probability RMSEA <= .05 1.000
CFI/TLI !@ CFI/TFI的结果
CFI 0.997 !@ CFI的结果
TLI 0.997 !@ TLI的结果
Chi-Square Test of Model Fit for the Baseline Model !@ 基准模型(基线模型)的卡方检验结果
Value 1524.403 !@ 卡方值
Degrees of Freedom 66 !@ 自由度
P-Value 0.0000 !@ 显著性
SRMR (Standardized Root Mean Square Residual) !@ SRMR的结果
Value 0.027
MODEL RESULTS !@ 模型结果,非标准化的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 BY
Y1 1.000 0.000 999.000 999.000 !@ Y1的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
Y2 1.183 0.104 11.376 0.000 !@ Y2的非标准化因子负荷
Y3 0.938 0.087 10.818 0.000 !@ Y3的非标准化因子负荷
F2 BY
Y4 1.000 0.000 999.000 999.000 !@ Y4的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
Y5 0.870 0.085 10.202 0.000 !@ Y2的非标准化因子负荷
Y6 0.891 0.092 9.735 0.000 !@ Y3的非标准化因子负荷
F3 BY
Y7 1.000 0.000 999.000 999.000 !@ Y7的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
Y8 0.872 0.059 14.699 0.000 !@ Y8的非标准化因子负荷
Y9 0.882 0.060 14.611 0.000 !@ Y9的非标准化因子负荷
F4 BY
Y10 1.000 0.000 999.000 999.000 !@ Y10的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
Y11 0.826 0.094 8.812 0.000 !@ Y11的非标准化因子负荷
Y12 0.682 0.089 7.696 0.000 !@ Y12的非标准化因子负荷
F4 ON
F3 0.473 0.057 8.306 0.000 !@ F3到F4的系数
F3 ON
F1 0.563 0.070 8.027 0.000 !@ F1到F3的系数
F2 0.790 0.086 9.228 0.000 !@ F1到F3的系数
F2 WITH
F1 -0.030 0.055 -0.545 0.586 !@ F1 F2之间的相关系数
Intercepts !@ 截距,潜变量为0时,观察变量的值
Y1 0.011 0.062 0.183 0.855 !@ Y1的截距
Y2 0.047 0.064 0.738 0.460 !@ Y2的截距
Y3 0.005 0.062 0.078 0.938 !@ Y3的截距
Y4 0.104 0.064 1.627 0.104 !@ Y4的截距
Y5 0.078 0.057 1.361 0.173 !@ Y5的截距
Y6 0.074 0.059 1.241 0.215 !@ Y6的截距
Y7 0.051 0.068 0.754 0.451 !@ Y7的截距
Y8 0.063 0.063 1.000 0.317 !@ Y8的截距
Y9 0.078 0.063 1.248 0.212 !@ Y9的截距
Y10 -0.008 0.064 -0.128 0.898 !@ Y10的截距
Y11 0.039 0.055 0.716 0.474 !@ Y11的截距
Y12 0.031 0.054 0.563 0.574 !@ Y12的截距
Variances !@ 因子方差
F1 0.884 0.122 7.234 0.000 !@ F1的方差,999.000代表没有计算,也就是没有这个结果(下同)
F2 0.888 0.130 6.830 0.000 !@ F2的方差,999.000代表没有计算,也就是没有这个结果(下同)
Residual Variances !@ 残差,潜变量未能解释的方差
Y1 1.033 0.094 11.034 0.000 !@ Y1的残差
Y2 0.795 0.101 7.862 0.000 !@ Y2的残差
Y3 1.137 0.092 12.389 0.000 !@ Y3的残差
Y4 1.151 0.104 11.039 0.000 !@ Y4的残差
Y5 0.950 0.083 11.468 0.000 !@ Y5的残差
Y6 1.056 0.091 11.670 0.000 !@ Y6的残差
Y7 0.954 0.089 10.762 0.000 !@ Y7的残差
Y8 0.945 0.079 11.980 0.000 !@ Y8的残差
Y9 0.896 0.077 11.581 0.000 !@ Y9的残差
Y10 1.202 0.118 10.193 0.000 !@ Y10的残差
Y11 0.916 0.085 10.777 0.000 !@ Y11的残差
Y12 1.071 0.083 12.834 0.000 !@ Y12的残差
F3 0.550 0.092 5.961 0.000 !@ F3的残差
F4 0.555 0.102 5.422 0.000 !@ F4的残差
STANDARDIZED MODEL RESULTS !@ 模型结果,标准化的结果
STDYX Standardization !@ 观测变量、潜变量均标准化后的结果,也就是全部标准化后的结果。一般报告这个结果。
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 BY
Y1 0.679 0.035 19.246 0.000 !@ Y1的标准化因子负荷
Y2 0.780 0.033 23.806 0.000 !@ Y2的标准化因子负荷
Y3 0.637 0.035 18.004 0.000 !@ Y3的标准化因子负荷
F2 BY
Y4 0.660 0.038 17.593 0.000 !@ Y4的标准化因子负荷
Y5 0.644 0.038 17.002 0.000 !@ Y5的标准化因子负荷
Y6 0.633 0.038 16.496 0.000 !@ Y6的标准化因子负荷
F3 BY
Y7 0.766 0.026 29.462 0.000 !@ Y7的标准化因子负荷
Y8 0.723 0.028 25.845 0.000 !@ Y8的标准化因子负荷
Y9 0.736 0.028 26.747 0.000 !@ Y9的标准化因子负荷
F4 BY
Y10 0.646 0.043 15.098 0.000 !@ Y10的标准化因子负荷
Y11 0.625 0.043 14.546 0.000 !@ Y11的标准化因子负荷
Y12 0.521 0.046 11.444 0.000 !@ Y12的标准化因子负荷
F4 ON
F3 0.595 0.049 12.145 0.000 !@ F3到F4的系数
F3 ON
F1 0.454 0.048 9.535 0.000 !@ F1到F3的系数
F2 0.639 0.044 14.485 0.000 !@ F2到F3的系数
F2 WITH
F1 -0.034 0.062 -0.545 0.586 !@ F1 F2之间的相关系数
Intercepts !@ 截距,潜变量为0时,观察变量的值
Y1 0.008 0.045 0.183 0.855 !@ Y1的截距
Y2 0.033 0.045 0.738 0.460 !@ Y2的截距
Y3 0.003 0.045 0.078 0.938 !@ Y3的截距
Y4 0.073 0.045 1.625 0.104 !@ Y4的截距
Y5 0.061 0.045 1.360 0.174 !@ Y5的截距
Y6 0.055 0.045 1.240 0.215 !@ Y6的截距
Y7 0.034 0.045 0.754 0.451 !@ Y7的截距
Y8 0.045 0.045 0.999 0.318 !@ Y8的截距
Y9 0.056 0.045 1.247 0.212 !@ Y9的截距
Y10 -0.006 0.045 -0.128 0.898 !@ Y10的截距
Y11 0.032 0.045 0.716 0.474 !@ Y11的截距
Y12 0.025 0.045 0.563 0.574 !@ Y12的截距
Variances !@ 因子方差
F1 1.000 0.000 999.000 999.000 !@ F1的方差。999.000代表没有计算,也就是没有这个结果(下同)
F2 1.000 0.000 999.000 999.000 !@ F2的方差。999.000代表没有计算,也就是没有这个结果(下同)
Residual Variances !@ 残差,潜变量未能解释的方差
Y1 0.539 0.048 11.249 0.000 !@ Y1的残差
Y2 0.392 0.051 7.660 0.000 !@ Y2的残差
Y3 0.594 0.045 13.174 0.000 !@ Y3的残差
Y4 0.565 0.050 11.403 0.000 !@ Y4的残差
Y5 0.586 0.049 12.024 0.000 !@ Y5的残差
Y6 0.600 0.049 12.361 0.000 !@ Y6的残差
Y7 0.413 0.040 10.352 0.000 !@ Y7的残差
Y8 0.478 0.040 11.832 0.000 !@ Y8的残差
Y9 0.459 0.040 11.333 0.000 !@ Y9的残差
Y10 0.583 0.055 10.565 0.000 !@ Y10的残差
Y11 0.610 0.054 11.374 0.000 !@ Y11的残差
Y12 0.728 0.047 15.351 0.000 !@ Y12的残差
F3 0.405 0.056 7.206 0.000 !@ F3的残差
F4 0.646 0.058 11.088 0.000 !@ F4的残差
STDY Standardization !@ 观测变量标准化后的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 BY
Y1 0.679 0.035 19.246 0.000 !@ Y1的标准化因子负荷
Y2 0.780 0.033 23.806 0.000 !@ Y2的标准化因子负荷
Y3 0.637 0.035 18.004 0.000 !@ Y3的标准化因子负荷
F2 BY
Y4 0.660 0.038 17.593 0.000 !@ Y4的标准化因子负荷
Y5 0.644 0.038 17.002 0.000 !@ Y5的标准化因子负荷
Y6 0.633 0.038 16.496 0.000 !@ Y6的标准化因子负荷
F3 BY
Y7 0.766 0.026 29.462 0.000 !@ Y7的标准化因子负荷
Y8 0.723 0.028 25.845 0.000 !@ Y8的标准化因子负荷
Y9 0.736 0.028 26.747 0.000 !@ Y9的标准化因子负荷
F4 BY
Y10 0.646 0.043 15.098 0.000 !@ Y10的标准化因子负荷
Y11 0.625 0.043 14.546 0.000 !@ Y11的标准化因子负荷
Y12 0.521 0.046 11.444 0.000 !@ Y12的标准化因子负荷
F4 ON
F3 0.595 0.049 12.145 0.000 !@ F3到F4的系数
F3 ON
F1 0.454 0.048 9.535 0.000 !@ F1到F3的系数
F2 0.639 0.044 14.485 0.000 !@ F2到F3的系数
F2 WITH
F1 -0.034 0.062 -0.545 0.586 !@ F1 F2之间的相关系数
Intercepts !@ 截距,潜变量为0时,观察变量的值
Y1 0.008 0.045 0.183 0.855 !@ Y1的截距
Y2 0.033 0.045 0.738 0.460 !@ Y2的截距
Y3 0.003 0.045 0.078 0.938 !@ Y3的截距
Y4 0.073 0.045 1.625 0.104 !@ Y4的截距
Y5 0.061 0.045 1.360 0.174 !@ Y5的截距
Y6 0.055 0.045 1.240 0.215 !@ Y6的截距
Y7 0.034 0.045 0.754 0.451 !@ Y7的截距
Y8 0.045 0.045 0.999 0.318 !@ Y8的截距
Y9 0.056 0.045 1.247 0.212 !@ Y9的截距
Y10 -0.006 0.045 -0.128 0.898 !@ Y10的截距
Y11 0.032 0.045 0.716 0.474 !@ Y11的截距
Y12 0.025 0.045 0.563 0.574 !@ Y12的截距
Variances !@ 因子方差
F1 1.000 0.000 999.000 999.000 !@ F1的方差。999.000代表没有计算,也就是没有这个结果(下同)
F2 1.000 0.000 999.000 999.000 !@ F2的方差。999.000代表没有计算,也就是没有这个结果(下同)
Residual Variances !@ 残差,潜变量未能解释的方差
Y1 0.539 0.048 11.249 0.000 !@ Y1的残差
Y2 0.392 0.051 7.660 0.000 !@ Y2的残差
Y3 0.594 0.045 13.174 0.000 !@ Y3的残差
Y4 0.565 0.050 11.403 0.000 !@ Y4的残差
Y5 0.586 0.049 12.024 0.000 !@ Y5的残差
Y6 0.600 0.049 12.361 0.000 !@ Y6的残差
Y7 0.413 0.040 10.352 0.000 !@ Y7的残差
Y8 0.478 0.040 11.832 0.000 !@ Y8的残差
Y9 0.459 0.040 11.333 0.000 !@ Y9的残差
Y10 0.583 0.055 10.565 0.000 !@ Y10的残差
Y11 0.610 0.054 11.374 0.000 !@ Y11的残差
Y12 0.728 0.047 15.351 0.000 !@ Y12的残差
F3 0.405 0.056 7.206 0.000 !@ F3的残差
F4 0.646 0.058 11.088 0.000 !@ F4的残差
STD Standardization !@ 潜变量标准化后的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 BY
Y1 0.940 0.065 14.467 0.000 !@ Y1的标准化因子负荷
Y2 1.112 0.066 16.789 0.000 !@ Y2的标准化因子负荷
Y3 0.881 0.064 13.771 0.000 !@ Y3的标准化因子负荷
F2 BY
Y4 0.942 0.069 13.659 0.000 !@ Y4的标准化因子负荷
Y5 0.820 0.062 13.326 0.000 !@ Y5的标准化因子负荷
Y6 0.840 0.064 13.047 0.000 !@ Y6的标准化因子负荷
F3 BY
Y7 1.165 0.064 18.327 0.000 !@ Y7的标准化因子负荷
Y8 1.016 0.060 17.018 0.000 !@ Y8的标准化因子负荷
Y9 1.028 0.059 17.368 0.000 !@ Y9的标准化因子负荷
F4 BY
Y10 0.927 0.075 12.352 0.000 !@ Y10的标准化因子负荷
Y11 0.765 0.064 11.999 0.000 !@ Y11的标准化因子负荷
Y12 0.632 0.063 9.954 0.000 !@ Y12的标准化因子负荷
F4 ON
F3 0.595 0.049 12.145 0.000 !@ F3到F4的系数
F3 ON
F1 0.454 0.048 9.535 0.000 !@ F1到F3的系数
F2 0.639 0.044 14.485 0.000 !@ F2到F3的系数
F2 WITH
F1 -0.034 0.062 -0.545 0.586 !@ F1 F2之间的相关系数
Intercepts !@ 截距,潜变量为0时,观察变量的值
Y1 0.011 0.062 0.183 0.855 !@ Y1的截距
Y2 0.047 0.064 0.738 0.460 !@ Y2的截距
Y3 0.005 0.062 0.078 0.938 !@ Y3的截距
Y4 0.104 0.064 1.627 0.104 !@ Y4的截距
Y5 0.078 0.057 1.361 0.173 !@ Y5的截距
Y6 0.074 0.059 1.241 0.215 !@ Y6的截距
Y7 0.051 0.068 0.754 0.451 !@ Y7的截距
Y8 0.063 0.063 1.000 0.317 !@ Y8的截距
Y9 0.078 0.063 1.248 0.212 !@ Y9的截距
Y10 -0.008 0.064 -0.128 0.898 !@ Y10的截距
Y11 0.039 0.055 0.716 0.474 !@ Y11的截距
Y12 0.031 0.054 0.563 0.574 !@ Y12的截距
Variances !@ 因子方差
F1 1.000 0.000 999.000 999.000 !@ F1的方差。999.000代表没有计算,也就是没有这个结果(下同)
F2 1.000 0.000 999.000 999.000 !@ F1的方差。999.000代表没有计算,也就是没有这个结果(下同)
Residual Variances !@ 残差,潜变量未能解释的方差
Y1 1.033 0.094 11.034 0.000 !@ Y1的残差
Y2 0.795 0.101 7.862 0.000 !@ Y2的残差
Y3 1.137 0.092 12.389 0.000 !@ Y3的残差
Y4 1.151 0.104 11.039 0.000 !@ Y4的残差
Y5 0.950 0.083 11.468 0.000 !@ Y5的残差
Y6 1.056 0.091 11.670 0.000 !@ Y6的残差
Y7 0.954 0.089 10.762 0.000 !@ Y7的残差
Y8 0.945 0.079 11.980 0.000 !@ Y8的残差
Y9 0.896 0.077 11.581 0.000 !@ Y9的残差
Y10 1.202 0.118 10.193 0.000 !@ Y10的残差
Y11 0.916 0.085 10.777 0.000 !@ Y11的残差
Y12 1.071 0.083 12.834 0.000 !@ Y12的残差
F3 0.405 0.056 7.206 0.000 !@ F3的残差
F4 0.646 0.058 11.088 0.000 !@ F4的残差
R-SQUARE !@ R的平方,观测变量、潜变量被因子解释的百分比
Observed Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value !@ 观测变量 估计值 标准误 估计标准误 P值(显著性)
Y1 0.461 0.048 9.623 0.000 !@ Y1被F1解释的百分比
Y2 0.608 0.051 11.903 0.000 !@ Y2被F1解释的百分比
Y3 0.406 0.045 9.002 0.000 !@ Y3被F1解释的百分比
Y4 0.435 0.050 8.797 0.000 !@ Y4被F2解释的百分比
Y5 0.414 0.049 8.501 0.000 !@ Y5被F2解释的百分比
Y6 0.400 0.049 8.248 0.000 !@ Y6被F2解释的百分比
Y7 0.587 0.040 14.731 0.000 !@ Y7被F3解释的百分比
Y8 0.522 0.040 12.923 0.000 !@ Y8被F3解释的百分比
Y9 0.541 0.040 13.373 0.000 !@ Y9被F3解释的百分比
Y10 0.417 0.055 7.549 0.000 !@ Y10被F4解释的百分比
Y11 0.390 0.054 7.273 0.000 !@ Y11被F4解释的百分比
Y12 0.272 0.047 5.722 0.000 !@ Y12被F4解释的百分比
Latent Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value !@ 潜变量 估计值 标准误 估计标准误 P值(显著性)
F3 0.595 0.056 10.581 0.000 !@ F3被F1、F2解释的百分比
F4 0.354 0.058 6.073 0.000 !@ F4被F3解释的百分比
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.448E-01 !@ 信息矩阵的条件数
(ratio of smallest to largest eigenvalue)
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS !@总效应,总间接效应,具体间接效应和直接效应
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Effects from F1 to F4 !@F1到F4的影响
Indirect 0.266 0.043 6.144 0.000
STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS !@标准化总效应,总间接效应,具体间接效应和直接效应
STDYX Standardization !@ 观测变量、潜变量均标准化后的结果,也就是全部标准化后的结果。一般报告这个结果。
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Effects from F1 to F4 !@F1到F4的影响
Indirect 0.270 0.036 7.478 0.000
STDY Standardization !@ 观测变量标准化后的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Effects from F1 to F4 !@F1到F4的影响
Indirect 0.270 0.036 7.478 0.000
STD Standardization !@ 潜变量标准化后的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Effects from F1 to F4 !@F1到F4的影响
Indirect 0.270 0.036 7.478 0.000
DIAGRAM INFORMATION !@ 图形信息
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram. !@ 在Diagram菜单下显示图形信息
If running Mplus from the Mplus Diagrammer, the diagram opens automatically. !@ 如果是从Mplus Diagrammer运行Mplus,会自动显示图形信息
Diagram output !图形输出路径
c:\program files\mplus\mplus examples\user's guide examples\ex5.12.dgm
Beginning Time: 12:30:10 !@ 命令语句(程序)开始运行时间
Ending Time: 12:30:12 !@ 命令语句(程序)结束运行时间
Elapsed Time: 00:00:02 !@ 程序运行花费时间