“Mplus Path Analysis Example 3.11”的版本间的差异
来自OBHRM百科
Lichaoping(讨论 | 贡献) (创建页面,内容为“==示意图== center ==代码与注释==”) |
Lichaoping(讨论 | 贡献) |
||
| (未显示2个用户的5个中间版本) | |||
| 第2行: | 第2行: | ||
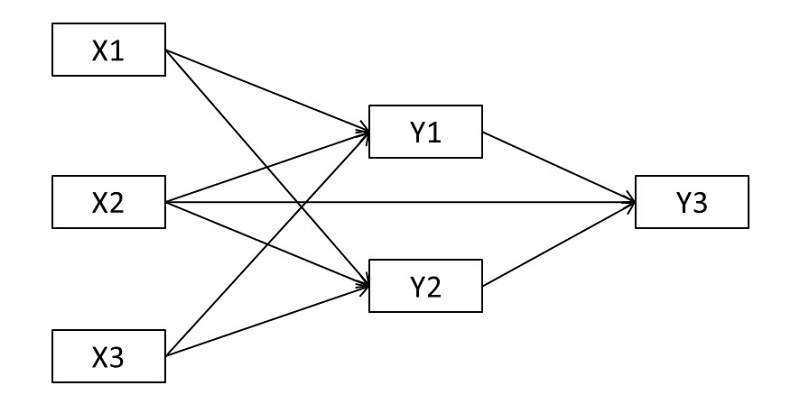
[[文件:0311.jpg | center ]] | [[文件:0311.jpg | center ]] | ||
==代码与注释== | ==代码与注释== | ||
| + | <pre>TITLE: this is an example of a path analysis ! 标题 | ||
| + | with continuous dependent variables | ||
| + | DATA: FILE IS ex3.11.dat; ! 数据文件 | ||
| + | VARIABLE:NAMES ARE y1-y3 x1-x3; ! 数据文件中变量的名称,按顺序:y1,y2,y3,x1,x2,x3 | ||
| + | MODEL: y1 y2 ON x1 x2 x3; ! x1,x2,x3分别到y1,y2的回归 | ||
| + | y3 ON y1 y2 x2; ! x2,y1,y2到y3的回归 | ||
| + | OUTPUT: STANDARDIZED; ! 结果:标准化结果。</pre> | ||
| + | |||
| + | ==结果== | ||
| + | <pre>INPUT INSTRUCTIONS !@ 输入的命令语句,会全部显示,下面几行就是输入的命令语句 | ||
| + | |||
| + | TITLE: this is an example of a path analysis ! 这是标题,总共两行内容,第一行 | ||
| + | with continuous dependent variables ! 第二行,想要多少行,就写多少行 | ||
| + | DATA: FILE IS ex3.11.dat; ! 读数据文件,文件名要正确,文件路径与对应的分析程序在同一目录下;或标明绝对路径,比如:c:\mplus\ex3.11.dat。 | ||
| + | VARIABLE:NAMES ARE y1-y3 x1-x3; ! 数据文件中变量的名称,按顺序:y1,y2,y3,x1,x2,x3 | ||
| + | MODEL: y1 y2 ON x1 x2 x3; ! x1,x2,x3分别到y1,y2的回归 | ||
| + | y3 ON y1 y2 x2; ! x2,y1,y2到y3的回归 | ||
| + | OUTPUT: STANDARDIZED; ! 结果:标准化结果。 | ||
| + | |||
| + | |||
| + | |||
| + | *** WARNING | ||
| + | Input line exceeded 90 characters. Some input may be truncated. !@ 警告:命令语句的第四行太长,只保留了前90个字符,但是不影响结果 | ||
| + | VARIABLE:NAMES ARE y1-y3 x1-x3; ! 数据文件中变量的名称,按顺序:y1,y2,y3,x1,x2,x3 | ||
| + | 1 WARNING(S) FOUND IN THE INPUT INSTRUCTIONS | ||
| + | |||
| + | |||
| + | |||
| + | this is an example of a path analysis !@ TITLE,标题 | ||
| + | with continuous dependent variables ! 第二行,想要多少行,就写多少行 | ||
| + | |||
| + | SUMMARY OF ANALYSIS !@分析总体情况 | ||
| + | |||
| + | Number of groups 1 !@ 1组数据,也就是样本没有分组 | ||
| + | Number of observations 500 !@ 样本量500 | ||
| + | |||
| + | Number of dependent variables 3 !@ (因)变量3个 | ||
| + | Number of independent variables 3 !@ (自)变量3个 | ||
| + | Number of continuous latent variables 0 !@ 潜变量0个 | ||
| + | |||
| + | Observed dependent variables !@ 观测(因)变量 | ||
| + | |||
| + | Continuous !@ 观测(因)变量为连续变量 Y1 Y2 Y3 | ||
| + | Y1 Y2 Y3 | ||
| + | |||
| + | Observed independent variables !@ 观测(自)变量 X1 X2 X3 | ||
| + | X1 X2 X3 | ||
| + | |||
| + | |||
| + | Estimator ML !@ 估计方法:最大似然法 | ||
| + | Information matrix OBSERVED !@ 信息矩阵:观测数据 | ||
| + | Maximum number of iterations 1000 !@ 最大迭代次数1000次 | ||
| + | Convergence criterion 0.500D-04 !@ 聚合标准(或翻译为收敛标准) | ||
| + | Maximum number of steepest descent iterations 20 !@ 迭代下降最大数:20 | ||
| + | |||
| + | Input data file(s) !@ 输入文件:ex3.11.dat | ||
| + | ex3.11.dat; | ||
| + | |||
| + | Input data format FREE !@ 输入文件格式:自由格式,这是Mplus的默认格式 | ||
| + | |||
| + | |||
| + | |||
| + | THE MODEL ESTIMATION TERMINATED NORMALLY !@ 模型估计正常终止,如果是非正常终止,就需要检查数据或命令语句 | ||
| + | |||
| + | |||
| + | |||
| + | MODEL FIT INFORMATION !@ 模型拟合指数 | ||
| + | |||
| + | Number of Free Parameters 15 !@ 自由参数的个数:15个 | ||
| + | |||
| + | Loglikelihood !@ 似然函数值的自然对数 | ||
| + | |||
| + | H0 Value -2364.002 | ||
| + | H1 Value -2363.623 | ||
| + | |||
| + | Information Criteria !@ 信息标准 | ||
| + | |||
| + | Akaike (AIC) 4758.004 !@ AIC | ||
| + | Bayesian (BIC) 4821.223 !@ BIC | ||
| + | Sample-Size Adjusted BIC 4773.612 !@ 考虑样本量调整后的BIC值 | ||
| + | (n* = (n + 2) / 24) | ||
| + | |||
| + | Chi-Square Test of Model Fit !@ 卡方检验的结果 | ||
| + | |||
| + | Value 0.757 !@ 卡方值 | ||
| + | Degrees of Freedom 3 !@ 自由度 | ||
| + | P-Value 0.8598 !@ 显著性 | ||
| + | |||
| + | RMSEA (Root Mean Square Error Of Approximation) !@ RMSEA的结果 | ||
| + | |||
| + | Estimate 0.000 !@ RMSEA的值 | ||
| + | 90 Percent C.I. 0.000 0.040 !@ RMSEA的90%置信区间 | ||
| + | Probability RMSEA <= .05 0.972 | ||
| + | |||
| + | CFI/TLI !@ CFI/TFI的结果 | ||
| + | |||
| + | CFI 1.000 !@ CFI的结果 | ||
| + | TLI 1.002 !@ TLI的结果 | ||
| + | |||
| + | Chi-Square Test of Model Fit for the Baseline Model !@ 基准模型(基线模型)的卡方检验结果 | ||
| + | |||
| + | Value 4107.449 !@ 卡方值 | ||
| + | Degrees of Freedom 12 !@ 自由度 | ||
| + | P-Value 0.0000 !@ 显著性 | ||
| + | |||
| + | SRMR (Standardized Root Mean Square Residual) !@ SRMR的结果 | ||
| + | |||
| + | Value 0.001 | ||
| + | |||
| + | |||
| + | |||
| + | MODEL RESULTS !@ 模型结果,非标准化的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Y1 ON | ||
| + | X1 0.992 0.043 22.979 0.000 !@ X1对Y1的非标准化回归系数(路径系数,下同) | ||
| + | X2 2.001 0.045 44.618 0.000 !@ X2对Y1的非标准化回归系数 | ||
| + | X3 3.052 0.045 68.274 0.000 !@ X3对Y1的非标准化回归系数 | ||
| + | |||
| + | Y2 ON | ||
| + | X1 2.935 0.050 59.002 0.000 !@ X1对Y2的非标准化回归系数 | ||
| + | X2 1.992 0.052 38.556 0.000 !@ X2对Y2的非标准化回归系数 | ||
| + | X3 1.023 0.051 19.869 0.000 !@ X3对Y2的非标准化回归系数 | ||
| + | |||
| + | Y3 ON | ||
| + | Y1 0.507 0.020 25.491 0.000 !@ Y1对Y3的非标准化回归系数 | ||
| + | Y2 0.746 0.020 37.914 0.000 !@ Y2对Y3的非标准化回归系数 | ||
| + | X2 1.046 0.072 14.540 0.000 !@ X2对Y3的非标准化回归系数 | ||
| + | |||
| + | Intercepts !@ 截距,自变量为0时,因变量的值 | ||
| + | Y1 -1.064 0.046 -23.059 0.000 !@ Y1的截距 | ||
| + | Y2 -0.042 0.053 -0.784 0.433 !@ Y2的截距 | ||
| + | Y3 1.068 0.063 17.093 0.000 !@ Y3的截距 | ||
| + | |||
| + | Residual Variances !@ 残差,因变量未能解释的方差 | ||
| + | Y1 1.061 0.067 15.811 0.000 !@ Y1的残差 | ||
| + | Y2 1.408 0.089 15.811 0.000 !@ Y2的残差 | ||
| + | Y3 1.717 0.109 15.811 0.000 !@ Y3的残差 | ||
| + | |||
| + | |||
| + | STANDARDIZED MODEL RESULTS !@ 模型结果,标准化的结果 | ||
| + | |||
| + | |||
| + | STDYX Standardization !@ 自变量和因变量均标准化后的结果,也就是全部标准化后的结果。一般报告这个结果。 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Y1 ON | ||
| + | X1 0.254 0.015 16.801 0.000 !@ X1对Y1的标准化回归系数 | ||
| + | X2 0.495 0.020 24.957 0.000 !@ X2对Y1的标准化回归系数 | ||
| + | X3 0.758 0.020 37.078 0.000 !@ X3对Y1的标准化回归系数 | ||
| + | |||
| + | Y2 ON | ||
| + | X1 0.759 0.021 35.491 0.000 !@ X1对Y2的标准化回归系数 | ||
| + | X2 0.497 0.021 23.938 0.000 !@ X2对Y2的标准化回归系数 | ||
| + | X3 0.256 0.016 15.680 0.000 !@ X3对Y2的标准化回归系数 | ||
| + | |||
| + | Y3 ON | ||
| + | Y1 0.375 0.016 23.022 0.000 !@ Y1对Y3的标准化回归系数 | ||
| + | Y2 0.547 0.016 34.161 0.000 !@ Y2对Y3的标准化回归系数 | ||
| + | X2 0.192 0.014 13.462 0.000 !@ X2对Y3的标准化回归系数 | ||
| + | |||
| + | Intercepts !@ 截距,自变量为0时,因变量的值 | ||
| + | Y1 -0.255 0.014 -18.599 0.000 !@ Y1的截距 | ||
| + | Y2 -0.010 0.013 -0.784 0.433 !@ Y2的截距 | ||
| + | Y3 0.190 0.012 15.238 0.000 !@ Y3的截距 | ||
| + | |||
| + | Residual Variances !@ 残差,因变量未能解释的方差 | ||
| + | Y1 0.061 0.005 11.537 0.000 !@ Y1的残差 | ||
| + | Y2 0.082 0.007 11.671 0.000 !@ Y2的残差 | ||
| + | Y3 0.054 0.005 11.497 0.000 !@ Y3的残差 | ||
| + | |||
| + | |||
| + | STDY Standardization !@ 因变量标准化后的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Y1 ON | ||
| + | X1 0.238 0.012 19.425 0.000 !@ X1对Y1的标准化回归系数 | ||
| + | X2 0.479 0.017 28.186 0.000 !@ X2对Y1的标准化回归系数 | ||
| + | X3 0.731 0.023 32.092 0.000 !@ X3对Y1的标准化回归系数 | ||
| + | |||
| + | Y2 ON | ||
| + | X1 0.710 0.022 32.309 0.000 !@ X1对Y2的标准化回归系数 | ||
| + | X2 0.482 0.018 27.283 0.000 !@ X2对Y2的标准化回归系数 | ||
| + | X3 0.247 0.014 17.668 0.000 !@ X3对Y2的标准化回归系数 | ||
| + | |||
| + | Y3 ON | ||
| + | Y1 0.375 0.016 23.022 0.000 !@ Y1对Y3的标准化回归系数 | ||
| + | Y2 0.547 0.016 34.161 0.000 !@ Y2对Y3的标准化回归系数 | ||
| + | X2 0.186 0.014 13.468 0.000 !@ X2对Y3的标准化回归系数 | ||
| + | |||
| + | Intercepts !@ 截距,自变量为0时,因变量的值 | ||
| + | Y1 -0.255 0.014 -18.599 0.000 !@ Y1的截距 | ||
| + | Y2 -0.010 0.013 -0.784 0.433 !@ Y2的截距 | ||
| + | Y3 0.190 0.012 15.238 0.000 !@ Y3的截距 | ||
| + | |||
| + | Residual Variances !@ 残差,因变量未能解释的方差 | ||
| + | Y1 0.061 0.005 11.537 0.000 !@ Y1的残差 | ||
| + | Y2 0.082 0.007 11.671 0.000 !@ Y2的残差 | ||
| + | Y3 0.054 0.005 11.497 0.000 !@ Y3的残差 | ||
| + | |||
| + | |||
| + | STD Standardization !@ 自变量标准化后的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Y1 ON | ||
| + | X1 0.992 0.043 22.979 0.000 !@ X1对Y1的标准化回归系数 | ||
| + | X2 2.001 0.045 44.618 0.000 !@ X2对Y1的标准化回归系数 | ||
| + | X3 3.052 0.045 68.274 0.000 !@ X3对Y1的标准化回归系数 | ||
| + | |||
| + | Y2 ON | ||
| + | X1 2.935 0.050 59.002 0.000 !@ X1对Y2的标准化回归系数 | ||
| + | X2 1.992 0.052 38.556 0.000 !@ X2对Y2的标准化回归系数 | ||
| + | X3 1.023 0.051 19.869 0.000 !@ X3对Y2的标准化回归系数 | ||
| + | |||
| + | Y3 ON | ||
| + | Y1 0.507 0.020 25.491 0.000 !@ Y1对Y3的标准化回归系数 | ||
| + | Y2 0.746 0.020 37.914 0.000 !@ Y2对Y3的标准化回归系数 | ||
| + | X2 1.046 0.072 14.540 0.000 !@ X2对Y3的标准化回归系数 | ||
| + | |||
| + | Intercepts !@ 截距,自变量为0时,因变量的值 | ||
| + | Y1 -1.064 0.046 -23.059 0.000 !@ Y1的截距 | ||
| + | Y2 -0.042 0.053 -0.784 0.433 !@ Y2的截距 | ||
| + | Y3 1.068 0.063 17.093 0.000 !@ Y3的截距 | ||
| + | |||
| + | Residual Variances !@ 残差,因变量未能解释的方差 | ||
| + | Y1 1.061 0.067 15.811 0.000 !@ Y1的残差 | ||
| + | Y2 1.408 0.089 15.811 0.000 !@ Y2的残差 | ||
| + | Y3 1.717 0.109 15.811 0.000 !@ Y3的残差 | ||
| + | |||
| + | |||
| + | R-SQUARE !@ R的平方,因变量被自变量解释的百分比 | ||
| + | |||
| + | Observed Two-Tailed | ||
| + | Variable Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Y1 0.939 0.005 177.949 0.000 !@ Y1被X1,X2,X3解释的百分比 | ||
| + | Y2 0.918 0.007 130.104 0.000 !@ Y2被X1,X2,X3解释的百分比 | ||
| + | Y3 0.946 0.005 201.127 0.000 !@ Y3被Y1,Y2,X2解释的百分比 | ||
| + | |||
| + | |||
| + | QUALITY OF NUMERICAL RESULTS | ||
| + | |||
| + | Condition Number for the Information Matrix 0.979E-02 !@ 信息矩阵的条件数 | ||
| + | (ratio of smallest to largest eigenvalue) | ||
| + | |||
| + | |||
| + | DIAGRAM INFORMATION !@ 图形信息 | ||
| + | |||
| + | Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram. !@ 在Diagram菜单下显示图形信息 | ||
| + | If running Mplus from the Mplus Diagrammer, the diagram opens automatically. !@ 如果是从Mplus Diagrammer运行Mplus,会自动显示图形信息 | ||
| + | |||
| + | Diagram output | ||
| + | e:\2016\mplus\mptext2.dgm | ||
| + | |||
| + | Beginning Time: 21:59:39 !@ 命令语句(程序)开始运行时间 | ||
| + | Ending Time: 21:59:40 !@ 命令语句(程序)结束运行时间 | ||
| + | Elapsed Time: 00:00:01 !@ 程序运行花费时间</pre> | ||
2017年6月17日 (六) 16:43的最新版本
示意图
代码与注释
TITLE: this is an example of a path analysis ! 标题
with continuous dependent variables
DATA: FILE IS ex3.11.dat; ! 数据文件
VARIABLE:NAMES ARE y1-y3 x1-x3; ! 数据文件中变量的名称,按顺序:y1,y2,y3,x1,x2,x3
MODEL: y1 y2 ON x1 x2 x3; ! x1,x2,x3分别到y1,y2的回归
y3 ON y1 y2 x2; ! x2,y1,y2到y3的回归
OUTPUT: STANDARDIZED; ! 结果:标准化结果。
结果
INPUT INSTRUCTIONS !@ 输入的命令语句,会全部显示,下面几行就是输入的命令语句
TITLE: this is an example of a path analysis ! 这是标题,总共两行内容,第一行
with continuous dependent variables ! 第二行,想要多少行,就写多少行
DATA: FILE IS ex3.11.dat; ! 读数据文件,文件名要正确,文件路径与对应的分析程序在同一目录下;或标明绝对路径,比如:c:\mplus\ex3.11.dat。
VARIABLE:NAMES ARE y1-y3 x1-x3; ! 数据文件中变量的名称,按顺序:y1,y2,y3,x1,x2,x3
MODEL: y1 y2 ON x1 x2 x3; ! x1,x2,x3分别到y1,y2的回归
y3 ON y1 y2 x2; ! x2,y1,y2到y3的回归
OUTPUT: STANDARDIZED; ! 结果:标准化结果。
*** WARNING
Input line exceeded 90 characters. Some input may be truncated. !@ 警告:命令语句的第四行太长,只保留了前90个字符,但是不影响结果
VARIABLE:NAMES ARE y1-y3 x1-x3; ! 数据文件中变量的名称,按顺序:y1,y2,y3,x1,x2,x3
1 WARNING(S) FOUND IN THE INPUT INSTRUCTIONS
this is an example of a path analysis !@ TITLE,标题
with continuous dependent variables ! 第二行,想要多少行,就写多少行
SUMMARY OF ANALYSIS !@分析总体情况
Number of groups 1 !@ 1组数据,也就是样本没有分组
Number of observations 500 !@ 样本量500
Number of dependent variables 3 !@ (因)变量3个
Number of independent variables 3 !@ (自)变量3个
Number of continuous latent variables 0 !@ 潜变量0个
Observed dependent variables !@ 观测(因)变量
Continuous !@ 观测(因)变量为连续变量 Y1 Y2 Y3
Y1 Y2 Y3
Observed independent variables !@ 观测(自)变量 X1 X2 X3
X1 X2 X3
Estimator ML !@ 估计方法:最大似然法
Information matrix OBSERVED !@ 信息矩阵:观测数据
Maximum number of iterations 1000 !@ 最大迭代次数1000次
Convergence criterion 0.500D-04 !@ 聚合标准(或翻译为收敛标准)
Maximum number of steepest descent iterations 20 !@ 迭代下降最大数:20
Input data file(s) !@ 输入文件:ex3.11.dat
ex3.11.dat;
Input data format FREE !@ 输入文件格式:自由格式,这是Mplus的默认格式
THE MODEL ESTIMATION TERMINATED NORMALLY !@ 模型估计正常终止,如果是非正常终止,就需要检查数据或命令语句
MODEL FIT INFORMATION !@ 模型拟合指数
Number of Free Parameters 15 !@ 自由参数的个数:15个
Loglikelihood !@ 似然函数值的自然对数
H0 Value -2364.002
H1 Value -2363.623
Information Criteria !@ 信息标准
Akaike (AIC) 4758.004 !@ AIC
Bayesian (BIC) 4821.223 !@ BIC
Sample-Size Adjusted BIC 4773.612 !@ 考虑样本量调整后的BIC值
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit !@ 卡方检验的结果
Value 0.757 !@ 卡方值
Degrees of Freedom 3 !@ 自由度
P-Value 0.8598 !@ 显著性
RMSEA (Root Mean Square Error Of Approximation) !@ RMSEA的结果
Estimate 0.000 !@ RMSEA的值
90 Percent C.I. 0.000 0.040 !@ RMSEA的90%置信区间
Probability RMSEA <= .05 0.972
CFI/TLI !@ CFI/TFI的结果
CFI 1.000 !@ CFI的结果
TLI 1.002 !@ TLI的结果
Chi-Square Test of Model Fit for the Baseline Model !@ 基准模型(基线模型)的卡方检验结果
Value 4107.449 !@ 卡方值
Degrees of Freedom 12 !@ 自由度
P-Value 0.0000 !@ 显著性
SRMR (Standardized Root Mean Square Residual) !@ SRMR的结果
Value 0.001
MODEL RESULTS !@ 模型结果,非标准化的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Y1 ON
X1 0.992 0.043 22.979 0.000 !@ X1对Y1的非标准化回归系数(路径系数,下同)
X2 2.001 0.045 44.618 0.000 !@ X2对Y1的非标准化回归系数
X3 3.052 0.045 68.274 0.000 !@ X3对Y1的非标准化回归系数
Y2 ON
X1 2.935 0.050 59.002 0.000 !@ X1对Y2的非标准化回归系数
X2 1.992 0.052 38.556 0.000 !@ X2对Y2的非标准化回归系数
X3 1.023 0.051 19.869 0.000 !@ X3对Y2的非标准化回归系数
Y3 ON
Y1 0.507 0.020 25.491 0.000 !@ Y1对Y3的非标准化回归系数
Y2 0.746 0.020 37.914 0.000 !@ Y2对Y3的非标准化回归系数
X2 1.046 0.072 14.540 0.000 !@ X2对Y3的非标准化回归系数
Intercepts !@ 截距,自变量为0时,因变量的值
Y1 -1.064 0.046 -23.059 0.000 !@ Y1的截距
Y2 -0.042 0.053 -0.784 0.433 !@ Y2的截距
Y3 1.068 0.063 17.093 0.000 !@ Y3的截距
Residual Variances !@ 残差,因变量未能解释的方差
Y1 1.061 0.067 15.811 0.000 !@ Y1的残差
Y2 1.408 0.089 15.811 0.000 !@ Y2的残差
Y3 1.717 0.109 15.811 0.000 !@ Y3的残差
STANDARDIZED MODEL RESULTS !@ 模型结果,标准化的结果
STDYX Standardization !@ 自变量和因变量均标准化后的结果,也就是全部标准化后的结果。一般报告这个结果。
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Y1 ON
X1 0.254 0.015 16.801 0.000 !@ X1对Y1的标准化回归系数
X2 0.495 0.020 24.957 0.000 !@ X2对Y1的标准化回归系数
X3 0.758 0.020 37.078 0.000 !@ X3对Y1的标准化回归系数
Y2 ON
X1 0.759 0.021 35.491 0.000 !@ X1对Y2的标准化回归系数
X2 0.497 0.021 23.938 0.000 !@ X2对Y2的标准化回归系数
X3 0.256 0.016 15.680 0.000 !@ X3对Y2的标准化回归系数
Y3 ON
Y1 0.375 0.016 23.022 0.000 !@ Y1对Y3的标准化回归系数
Y2 0.547 0.016 34.161 0.000 !@ Y2对Y3的标准化回归系数
X2 0.192 0.014 13.462 0.000 !@ X2对Y3的标准化回归系数
Intercepts !@ 截距,自变量为0时,因变量的值
Y1 -0.255 0.014 -18.599 0.000 !@ Y1的截距
Y2 -0.010 0.013 -0.784 0.433 !@ Y2的截距
Y3 0.190 0.012 15.238 0.000 !@ Y3的截距
Residual Variances !@ 残差,因变量未能解释的方差
Y1 0.061 0.005 11.537 0.000 !@ Y1的残差
Y2 0.082 0.007 11.671 0.000 !@ Y2的残差
Y3 0.054 0.005 11.497 0.000 !@ Y3的残差
STDY Standardization !@ 因变量标准化后的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Y1 ON
X1 0.238 0.012 19.425 0.000 !@ X1对Y1的标准化回归系数
X2 0.479 0.017 28.186 0.000 !@ X2对Y1的标准化回归系数
X3 0.731 0.023 32.092 0.000 !@ X3对Y1的标准化回归系数
Y2 ON
X1 0.710 0.022 32.309 0.000 !@ X1对Y2的标准化回归系数
X2 0.482 0.018 27.283 0.000 !@ X2对Y2的标准化回归系数
X3 0.247 0.014 17.668 0.000 !@ X3对Y2的标准化回归系数
Y3 ON
Y1 0.375 0.016 23.022 0.000 !@ Y1对Y3的标准化回归系数
Y2 0.547 0.016 34.161 0.000 !@ Y2对Y3的标准化回归系数
X2 0.186 0.014 13.468 0.000 !@ X2对Y3的标准化回归系数
Intercepts !@ 截距,自变量为0时,因变量的值
Y1 -0.255 0.014 -18.599 0.000 !@ Y1的截距
Y2 -0.010 0.013 -0.784 0.433 !@ Y2的截距
Y3 0.190 0.012 15.238 0.000 !@ Y3的截距
Residual Variances !@ 残差,因变量未能解释的方差
Y1 0.061 0.005 11.537 0.000 !@ Y1的残差
Y2 0.082 0.007 11.671 0.000 !@ Y2的残差
Y3 0.054 0.005 11.497 0.000 !@ Y3的残差
STD Standardization !@ 自变量标准化后的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Y1 ON
X1 0.992 0.043 22.979 0.000 !@ X1对Y1的标准化回归系数
X2 2.001 0.045 44.618 0.000 !@ X2对Y1的标准化回归系数
X3 3.052 0.045 68.274 0.000 !@ X3对Y1的标准化回归系数
Y2 ON
X1 2.935 0.050 59.002 0.000 !@ X1对Y2的标准化回归系数
X2 1.992 0.052 38.556 0.000 !@ X2对Y2的标准化回归系数
X3 1.023 0.051 19.869 0.000 !@ X3对Y2的标准化回归系数
Y3 ON
Y1 0.507 0.020 25.491 0.000 !@ Y1对Y3的标准化回归系数
Y2 0.746 0.020 37.914 0.000 !@ Y2对Y3的标准化回归系数
X2 1.046 0.072 14.540 0.000 !@ X2对Y3的标准化回归系数
Intercepts !@ 截距,自变量为0时,因变量的值
Y1 -1.064 0.046 -23.059 0.000 !@ Y1的截距
Y2 -0.042 0.053 -0.784 0.433 !@ Y2的截距
Y3 1.068 0.063 17.093 0.000 !@ Y3的截距
Residual Variances !@ 残差,因变量未能解释的方差
Y1 1.061 0.067 15.811 0.000 !@ Y1的残差
Y2 1.408 0.089 15.811 0.000 !@ Y2的残差
Y3 1.717 0.109 15.811 0.000 !@ Y3的残差
R-SQUARE !@ R的平方,因变量被自变量解释的百分比
Observed Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Y1 0.939 0.005 177.949 0.000 !@ Y1被X1,X2,X3解释的百分比
Y2 0.918 0.007 130.104 0.000 !@ Y2被X1,X2,X3解释的百分比
Y3 0.946 0.005 201.127 0.000 !@ Y3被Y1,Y2,X2解释的百分比
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.979E-02 !@ 信息矩阵的条件数
(ratio of smallest to largest eigenvalue)
DIAGRAM INFORMATION !@ 图形信息
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram. !@ 在Diagram菜单下显示图形信息
If running Mplus from the Mplus Diagrammer, the diagram opens automatically. !@ 如果是从Mplus Diagrammer运行Mplus,会自动显示图形信息
Diagram output
e:\2016\mplus\mptext2.dgm
Beginning Time: 21:59:39 !@ 命令语句(程序)开始运行时间
Ending Time: 21:59:40 !@ 命令语句(程序)结束运行时间
Elapsed Time: 00:00:01 !@ 程序运行花费时间