“Mplus Second-Order CFA Example 5.6”的版本间的差异
来自OBHRM百科
Lichaoping(讨论 | 贡献) (→示意图) |
Lichaoping(讨论 | 贡献) |
||
| (未显示同一用户的5个中间版本) | |||
| 第1行: | 第1行: | ||
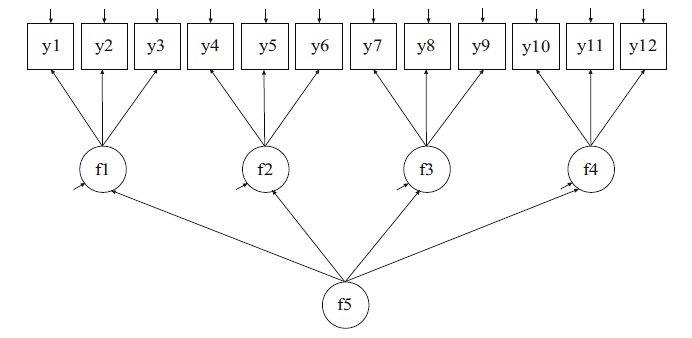
==示意图== | ==示意图== | ||
[[文件:mplus0506.JPG | center]] | [[文件:mplus0506.JPG | center]] | ||
| − | |||
==代码与注释== | ==代码与注释== | ||
<pre>TITLE: this is an example of a second-order factor analysis ! 这是标题 | <pre>TITLE: this is an example of a second-order factor analysis ! 这是标题 | ||
| 第10行: | 第9行: | ||
f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。 | f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。 | ||
f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。 | f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。 | ||
| − | f5 BY f1-f4; ! 二阶因素f5</pre> | + | f5 BY f1-f4; ! 二阶因素f5 |
| + | OUTPUT:STANDARDIZED; ! 报告标准化之后的结果,这是增加的命令语句</pre> | ||
| + | ==结果== | ||
| + | <pre>INPUT INSTRUCTIONS !@ 输入的命令语句,会全部显示,下面几行就是输入的命令语句 | ||
| + | |||
| + | TITLE: this is an example of a second-order factor analysis ! 这是标题 | ||
| + | DATA: FILE IS ex5.6.dat; ! 读数据文件,文件名要正确,文件路径与对应的分析程序在同一目录;或标明绝对路径,比如:c:\mplus\ex5.6.dat。 | ||
| + | VARIABLE: NAMES ARE y1-y12; ! 读取数据,该数据文件中包括12个变量的数据,变量名称可以自己。比如,可以是y1-y12,也可以是item1-item12。 | ||
| + | MODEL: f1 BY y1-y3; ! 定义第1个因素,该因素的测量指标有:y1,y2,y3。如果上面为item1-item6,则修改为item1-item3 | ||
| + | f2 BY y4-y6; ! 定义第2个因素,该因素的测量指标有:y4,y5,y6。 | ||
| + | f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。 | ||
| + | f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。 | ||
| + | f5 BY f1-f4; ! 定义第5个因素,该因素的测量指标有:f1,f2,f3,f4。 | ||
| + | OUTPUT:STANDARDIZED; ! 报告标准化之后的结果,这是增加的命令语句。 | ||
| + | |||
| + | |||
| + | |||
| + | INPUT READING TERMINATED NORMALLY !@ 数据读取正常 | ||
| + | |||
| + | |||
| + | |||
| + | this is an example of a second-order factor analysis !@ TITLE,标题 | ||
| + | |||
| + | SUMMARY OF ANALYSIS !@分析总体情况 | ||
| + | |||
| + | Number of groups 1 !@ 1组数据,也就是样本没有分组 | ||
| + | Number of observations 500 !@ 样本量500 | ||
| + | |||
| + | Number of dependent variables 12 !@ (因)变量12个 | ||
| + | Number of independent variables 0 !@ (自)变量0个 | ||
| + | Number of continuous latent variables 5 !@ 潜变量5个 | ||
| + | |||
| + | Observed dependent variables !@ 观测(因)变量 | ||
| + | |||
| + | Continuous !@ 观测(因)变量为连续变量 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10 Y11 Y12 | ||
| + | Y1 Y2 Y3 Y4 Y5 Y6 | ||
| + | Y7 Y8 Y9 Y10 Y11 Y12 | ||
| + | |||
| + | Continuous latent variables !@ 潜变量 F1 F2 F3 F4 F5 | ||
| + | F1 F2 F3 F4 F5 | ||
| + | |||
| + | |||
| + | Estimator ML !@ 估计方法:最大似然法 | ||
| + | Information matrix OBSERVED !@ 信息矩阵:观测数据 | ||
| + | Maximum number of iterations 1000 !@ 最大迭代次数1000次 | ||
| + | Convergence criterion 0.500D-04 !@ 聚合标准(或翻译为收敛标准) | ||
| + | Maximum number of steepest descent iterations 20 !@ 迭代下降最大数:20 | ||
| + | |||
| + | Input data file(s) !@ 输入文件:ex5.6.dat | ||
| + | ex5.6.dat | ||
| + | |||
| + | Input data format FREE !@ 输入文件格式:自由格式,这是Mplus的默认格式 | ||
| + | |||
| + | |||
| + | |||
| + | THE MODEL ESTIMATION TERMINATED NORMALLY !@ 模型估计正常终止,如果是非正常终止,就需要检查数据或命令语 | ||
| + | |||
| + | |||
| + | |||
| + | MODEL FIT INFORMATION !@ 模型拟合指数 | ||
| + | |||
| + | Number of Free Parameters 40 !@ 自由参数的个数:40个 | ||
| + | |||
| + | Loglikelihood !@ 似然函数值的自然对数 | ||
| + | |||
| + | H0 Value -7211.373 | ||
| + | H1 Value -7188.001 | ||
| + | |||
| + | Information Criteria !@ 信息标准 | ||
| + | |||
| + | Akaike (AIC) 14502.746 !@ AIC | ||
| + | Bayesian (BIC) 14671.330 !@ BIC | ||
| + | Sample-Size Adjusted BIC 14544.368 !@ 考虑样本量,调整后的BIC值 | ||
| + | (n* = (n + 2) / 24) | ||
| + | |||
| + | Chi-Square Test of Model Fit !@ 卡方检验的结果 | ||
| + | |||
| + | Value 46.743 !@ 卡方值 | ||
| + | Degrees of Freedom 50 !@ 自由度 | ||
| + | P-Value 0.6049 !@ 显著性 | ||
| + | |||
| + | RMSEA (Root Mean Square Error Of Approximation) !@ RMSEA的结果 | ||
| + | |||
| + | Estimate 0.000 !@ RMSEA的值 | ||
| + | 90 Percent C.I. 0.000 0.026 !@ RMSEA的90%置信区间 | ||
| + | Probability RMSEA <= .05 1.000 | ||
| + | |||
| + | CFI/TLI !@ CFI/TFI的结果 | ||
| + | |||
| + | CFI 1.000 !@ CFI的结果 | ||
| + | TLI 1.001 !@ TLI的结果 | ||
| + | |||
| + | Chi-Square Test of Model Fit for the Baseline Model !@ 基准模型(基线模型)的卡方检验结果 | ||
| + | |||
| + | Value 4012.035 !@ 卡方值 | ||
| + | Degrees of Freedom 66 !@ 自由度 | ||
| + | P-Value 0.0000 !@ 显著性 | ||
| + | |||
| + | SRMR (Standardized Root Mean Square Residual) !@ SRMR的结果 | ||
| + | |||
| + | Value 0.019 | ||
| + | |||
| + | |||
| + | |||
| + | MODEL RESULTS !@ 模型结果,非标准化的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 BY | ||
| + | Y1 1.000 0.000 999.000 999.000 !@ Y1的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | Y2 0.760 0.031 24.275 0.000 !@ Y2的非标准化因子负荷 | ||
| + | Y3 0.669 0.030 22.309 0.000 !@ Y3的非标准化因子负荷 | ||
| + | |||
| + | F2 BY | ||
| + | Y4 1.000 0.000 999.000 999.000 !@ Y4的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | Y5 0.718 0.030 23.976 0.000 !@ Y5的非标准化因子负荷 | ||
| + | Y6 0.703 0.031 22.853 0.000 !@ Y6的非标准化因子负荷 | ||
| + | |||
| + | F3 BY | ||
| + | Y7 1.000 0.000 999.000 999.000 !@ Y7的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | Y8 0.702 0.026 26.955 0.000 !@ Y8的非标准化因子负荷 | ||
| + | Y9 0.691 0.026 26.764 0.000 !@ Y9的非标准化因子负荷 | ||
| + | |||
| + | F4 BY | ||
| + | Y10 1.000 0.000 999.000 999.000 !@ Y10的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | Y11 0.742 0.029 25.350 0.000 !@ Y11的非标准化因子负荷 | ||
| + | Y12 0.669 0.029 23.461 0.000 !@ Y12的非标准化因子负荷 | ||
| + | |||
| + | F5 BY | ||
| + | F1 1.000 0.000 999.000 999.000 !@ F1的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | F2 0.944 0.148 6.397 0.000 !@ F2的非标准化因子负荷 | ||
| + | F3 1.168 0.179 6.516 0.000 !@ F3的非标准化因子负荷 | ||
| + | F4 0.854 0.139 6.142 0.000 !@ F4的非标准化因子负荷 | ||
| + | |||
| + | Intercepts !@ 截距,潜变量为0时,观察变量的值 | ||
| + | Y1 0.011 0.059 0.183 0.855 !@ Y1的截距 | ||
| + | Y2 0.028 0.046 0.617 0.537 !@ Y2的截距 | ||
| + | Y3 0.005 0.043 0.109 0.913 !@ Y3的截距 | ||
| + | Y4 0.100 0.060 1.652 0.099 !@ Y4的截距 | ||
| + | Y5 0.078 0.045 1.730 0.084 !@ Y5的截距 | ||
| + | Y6 0.076 0.046 1.671 0.095 !@ Y6的截距 | ||
| + | Y7 0.024 0.061 0.390 0.697 !@ Y7的截距 | ||
| + | Y8 0.025 0.046 0.545 0.585 !@ Y8的截距 | ||
| + | Y9 0.034 0.046 0.741 0.458 !@ Y9的截距 | ||
| + | Y10 -0.016 0.062 -0.261 0.794 !@ Y10的截距 | ||
| + | Y11 0.010 0.047 0.202 0.840 !@ Y11的截距 | ||
| + | Y12 0.006 0.045 0.134 0.894 !@ Y12的截距 | ||
| + | |||
| + | Variances !@ 因子方差 | ||
| + | F5 0.464 0.100 4.657 0.000 !@ F5的方差 | ||
| + | |||
| + | Residual Variances !@ 残差,潜变量未能解释的方差 | ||
| + | Y1 0.348 0.043 8.132 0.000 !@ Y1的残差 | ||
| + | Y2 0.251 0.027 9.465 0.000 !@ Y2的残差 | ||
| + | Y3 0.320 0.026 12.271 0.000 !@ Y3的残差 | ||
| + | Y4 0.366 0.045 8.187 0.000 !@ Y4的残差 | ||
| + | Y5 0.268 0.026 10.303 0.000 !@ Y5的残差 | ||
| + | Y6 0.330 0.028 11.636 0.000 !@ Y6的残差 | ||
| + | Y7 0.272 0.038 7.094 0.000 !@ Y7的残差 | ||
| + | Y8 0.282 0.025 11.445 0.000 !@ Y8的残差 | ||
| + | Y9 0.276 0.024 11.416 0.000 !@ Y9的残差 | ||
| + | Y10 0.362 0.045 8.107 0.000 !@ Y10的残差 | ||
| + | Y11 0.266 0.027 9.854 0.000 !@ Y11的残差 | ||
| + | Y12 0.323 0.027 11.991 0.000 !@ Y12的残差 | ||
| + | F1 0.913 0.103 8.855 0.000 !@ F1的残差 | ||
| + | F2 1.036 0.107 9.672 0.000 !@ F2的残差 | ||
| + | F3 0.984 0.119 8.237 0.000 !@ F3的残差 | ||
| + | F4 1.213 0.115 10.567 0.000 !@ F4的残差 | ||
| + | |||
| + | |||
| + | STANDARDIZED MODEL RESULTS !@ 模型结果,标准化的结果 | ||
| + | |||
| + | |||
| + | STDYX Standardization !@ 观测变量、潜变量均标准化后的结果,也就是全部标准化后的结果。一般报告这个结果。 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 BY | ||
| + | Y1 0.894 0.015 59.864 0.000 !@ Y1的标准化因子负荷 | ||
| + | Y2 0.872 0.016 55.160 0.000 !@ Y2的标准化因子负荷 | ||
| + | Y3 0.811 0.019 43.281 0.000 !@ Y3的标准化因子负荷 | ||
| + | |||
| + | F2 BY | ||
| + | Y4 0.894 0.015 60.275 0.000 !@ Y4的标准化因子负荷 | ||
| + | Y5 0.858 0.016 52.512 0.000 !@ Y5的标准化因子负荷 | ||
| + | Y6 0.828 0.018 46.167 0.000 !@ Y6的标准化因子负荷 | ||
| + | |||
| + | F3 BY | ||
| + | Y7 0.925 0.012 79.008 0.000 !@ Y7的标准化因子负荷 | ||
| + | Y8 0.859 0.015 57.876 0.000 !@ Y8的标准化因子负荷 | ||
| + | Y9 0.858 0.015 57.175 0.000 !@ Y9的标准化因子负荷 | ||
| + | |||
| + | F4 BY | ||
| + | Y10 0.900 0.014 64.368 0.000 !@ Y10的标准化因子负荷 | ||
| + | Y11 0.873 0.015 57.629 0.000 !@ Y11的标准化因子负荷 | ||
| + | Y12 0.826 0.018 46.877 0.000 !@ Y12的标准化因子负荷 | ||
| + | |||
| + | F5 BY | ||
| + | F1 0.580 0.053 10.851 0.000 !@ F1的标准化因子负荷 | ||
| + | F2 0.534 0.053 10.096 0.000 !@ F2的标准化因子负荷 | ||
| + | F3 0.626 0.053 11.779 0.000 !@ F3的标准化因子负荷 | ||
| + | F4 0.467 0.054 8.658 0.000 !@ F4的标准化因子负荷 | ||
| + | |||
| + | Intercepts !@ 截距,潜变量为0时,观察变量的值 | ||
| + | Y1 0.008 0.045 0.183 0.855 !@ Y1的截距 | ||
| + | Y2 0.028 0.045 0.617 0.537 !@ Y2的截距 | ||
| + | Y3 0.005 0.045 0.109 0.913 !@ Y3的截距 | ||
| + | Y4 0.074 0.045 1.650 0.099 !@ Y4的截距 | ||
| + | Y5 0.077 0.045 1.728 0.084 !@ Y5的截距 | ||
| + | Y6 0.075 0.045 1.668 0.095 !@ Y6的截距 | ||
| + | Y7 0.017 0.045 0.390 0.697 !@ Y7的截距 | ||
| + | Y8 0.024 0.045 0.545 0.585 !@ Y8的截距 | ||
| + | Y9 0.033 0.045 0.741 0.459 !@ Y9的截距 | ||
| + | Y10 -0.012 0.045 -0.261 0.794 !@ Y10的截距 | ||
| + | Y11 0.009 0.045 0.202 0.840 !@ Y11的截距 | ||
| + | Y12 0.006 0.045 0.134 0.894 !@ Y12的截距 | ||
| + | |||
| + | Variances !@ 因子方差 | ||
| + | F5 1.000 0.000 999.000 999.000 !@ F5的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | |||
| + | Residual Variances !@ 残差,潜变量未能解释的方差 | ||
| + | Y1 0.202 0.027 7.557 0.000 !@ Y1的残差 | ||
| + | Y2 0.240 0.028 8.689 0.000 !@ Y2的残差 | ||
| + | Y3 0.342 0.030 11.247 0.000 !@ Y3的残差 | ||
| + | Y4 0.201 0.026 7.601 0.000 !@ Y4的残差 | ||
| + | Y5 0.264 0.028 9.403 0.000 !@ Y5的残差 | ||
| + | Y6 0.315 0.030 10.621 0.000 !@ Y6的残差 | ||
| + | Y7 0.144 0.022 6.634 0.000 !@ Y7的残差 | ||
| + | Y8 0.261 0.026 10.236 0.000 !@ Y8的残差 | ||
| + | Y9 0.263 0.026 10.225 0.000 !@ Y9的残差 | ||
| + | Y10 0.189 0.025 7.516 0.000 !@ Y10的残差 | ||
| + | Y11 0.238 0.026 8.981 0.000 !@ Y11的残差 | ||
| + | Y12 0.317 0.029 10.901 0.000 !@ Y12的残差 | ||
| + | F1 0.663 0.062 10.679 0.000 !@ F1的残差 | ||
| + | F2 0.714 0.057 12.629 0.000 !@ F2的残差 | ||
| + | F3 0.609 0.066 9.155 0.000 !@ F3的残差 | ||
| + | F4 0.782 0.050 15.527 0.000 !@ F4的残差 | ||
| + | |||
| + | |||
| + | STDY Standardization !@ 观测变量标准化后的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 BY | ||
| + | Y1 0.894 0.015 59.864 0.000 !@ Y1的标准化因子负荷 | ||
| + | Y2 0.872 0.016 55.160 0.000 !@ Y2的标准化因子负荷 | ||
| + | Y3 0.811 0.019 43.281 0.000 !@ Y3的标准化因子负荷 | ||
| + | |||
| + | F2 BY | ||
| + | Y4 0.894 0.015 60.275 0.000 !@ Y4的标准化因子负荷 | ||
| + | Y5 0.858 0.016 52.512 0.000 !@ Y5的标准化因子负荷 | ||
| + | Y6 0.828 0.018 46.167 0.000 !@ Y6的标准化因子负荷 | ||
| + | |||
| + | F3 BY | ||
| + | Y7 0.925 0.012 79.008 0.000 !@ Y7的标准化因子负荷 | ||
| + | Y8 0.859 0.015 57.876 0.000 !@ Y8的标准化因子负荷 | ||
| + | Y9 0.858 0.015 57.175 0.000 !@ Y9的标准化因子负荷 | ||
| + | |||
| + | F4 BY | ||
| + | Y10 0.900 0.014 64.368 0.000 !@ Y10的标准化因子负荷 | ||
| + | Y11 0.873 0.015 57.629 0.000 !@ Y11的标准化因子负荷 | ||
| + | Y12 0.826 0.018 46.877 0.000 !@ Y12的标准化因子负荷 | ||
| + | |||
| + | F5 BY | ||
| + | F1 0.580 0.053 10.851 0.000 !@ F1的标准化因子负荷 | ||
| + | F2 0.534 0.053 10.096 0.000 !@ F2的标准化因子负荷 | ||
| + | F3 0.626 0.053 11.779 0.000 !@ F3的标准化因子负荷 | ||
| + | F4 0.467 0.054 8.658 0.000 !@ F4的标准化因子负荷 | ||
| + | |||
| + | Intercepts !@ 截距,潜变量为0时,观察变量的值 | ||
| + | Y1 0.008 0.045 0.183 0.855 !@ Y1的截距 | ||
| + | Y2 0.028 0.045 0.617 0.537 !@ Y2的截距 | ||
| + | Y3 0.005 0.045 0.109 0.913 !@ Y3的截距 | ||
| + | Y4 0.074 0.045 1.650 0.099 !@ Y4的截距 | ||
| + | Y5 0.077 0.045 1.728 0.084 !@ Y5的截距 | ||
| + | Y6 0.075 0.045 1.668 0.095 !@ Y6的截距 | ||
| + | Y7 0.017 0.045 0.390 0.697 !@ Y7的截距 | ||
| + | Y8 0.024 0.045 0.545 0.585 !@ Y8的截距 | ||
| + | Y9 0.033 0.045 0.741 0.459 !@ Y9的截距 | ||
| + | Y10 -0.012 0.045 -0.261 0.794 !@ Y10的截距 | ||
| + | Y11 0.009 0.045 0.202 0.840 !@ Y11的截距 | ||
| + | Y12 0.006 0.045 0.134 0.894 !@ Y12的截距 | ||
| + | |||
| + | Variances | ||
| + | F5 1.000 0.000 999.000 999.000 !@ F5的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | |||
| + | Residual Variances !@ 残差,潜变量未能解释的方差 | ||
| + | Y1 0.202 0.027 7.557 0.000 !@ Y1的残差 | ||
| + | Y2 0.240 0.028 8.689 0.000 !@ Y2的残差 | ||
| + | Y3 0.342 0.030 11.247 0.000 !@ Y3的残差 | ||
| + | Y4 0.201 0.026 7.601 0.000 !@ Y4的残差 | ||
| + | Y5 0.264 0.028 9.403 0.000 !@ Y5的残差 | ||
| + | Y6 0.315 0.030 10.621 0.000 !@ Y6的残差 | ||
| + | Y7 0.144 0.022 6.634 0.000 !@ Y7的残差 | ||
| + | Y8 0.261 0.026 10.236 0.000 !@ Y8的残差 | ||
| + | Y9 0.263 0.026 10.225 0.000 !@ Y9的残差 | ||
| + | Y10 0.189 0.025 7.516 0.000 !@ Y10的残差 | ||
| + | Y11 0.238 0.026 8.981 0.000 !@ Y11的残差 | ||
| + | Y12 0.317 0.029 10.901 0.000 !@ Y12的残差 | ||
| + | F1 0.663 0.062 10.679 0.000 !@ F1的残差 | ||
| + | F2 0.714 0.057 12.629 0.000 !@ F2的残差 | ||
| + | F3 0.609 0.066 9.155 0.000 !@ F3的残差 | ||
| + | F4 0.782 0.050 15.527 0.000 !@ F4的残差 | ||
| + | |||
| + | |||
| + | STD Standardization !@ 潜变量标准化后的结果 | ||
| + | |||
| + | Two-Tailed | ||
| + | Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 BY | ||
| + | Y1 1.174 0.048 24.382 0.000 !@ Y1的非标准化因子负荷 | ||
| + | Y2 0.892 0.038 23.520 0.000 !@ Y2的非标准化因子负荷 | ||
| + | Y3 0.785 0.037 21.235 0.000 !@ Y3的非标准化因子负荷 | ||
| + | |||
| + | F2 BY | ||
| + | Y4 1.204 0.049 24.412 0.000 !@ Y4的非标准化因子负荷 | ||
| + | Y5 0.864 0.038 23.002 0.000 !@ Y5的非标准化因子负荷 | ||
| + | Y6 0.847 0.039 21.825 0.000 !@ Y6的非标准化因子负荷 | ||
| + | |||
| + | F3 BY | ||
| + | Y7 1.272 0.048 26.282 0.000 !@ Y7的非标准化因子负荷 | ||
| + | Y8 0.893 0.038 23.433 0.000 !@ Y8的非标准化因子负荷 | ||
| + | Y9 0.879 0.038 23.359 0.000 !@ Y9的非标准化因子负荷 | ||
| + | |||
| + | F4 BY | ||
| + | Y10 1.245 0.050 24.845 0.000 !@ Y10的非标准化因子负荷 | ||
| + | Y11 0.924 0.039 23.727 0.000 !@ Y11的非标准化因子负荷 | ||
| + | Y12 0.834 0.038 21.875 0.000 !@ Y12的非标准化因子负荷 | ||
| + | X | ||
| + | F5 BY | ||
| + | F1 0.580 0.053 10.851 0.000 !@ F1的非标准化因子负荷 | ||
| + | F2 0.534 0.053 10.096 0.000 !@ F2的非标准化因子负荷 | ||
| + | F3 0.626 0.053 11.779 0.000 !@ F3的非标准化因子负荷 | ||
| + | F4 0.467 0.054 8.658 0.000 !@ F4的非标准化因子负荷 | ||
| + | |||
| + | Intercepts !@ 截距,潜变量为0时,观察变量的值 | ||
| + | Y1 0.011 0.059 0.183 0.855 !@ Y1的截距 | ||
| + | Y2 0.028 0.046 0.617 0.537 !@ Y2的截距 | ||
| + | Y3 0.005 0.043 0.109 0.913 !@ Y3的截距 | ||
| + | Y4 0.100 0.060 1.652 0.099 !@ Y4的截距 | ||
| + | Y5 0.078 0.045 1.730 0.084 !@ Y5的截距 | ||
| + | Y6 0.076 0.046 1.671 0.095 !@ Y6的截距 | ||
| + | Y7 0.024 0.061 0.390 0.697 !@ Y7的截距 | ||
| + | Y8 0.025 0.046 0.545 0.585 !@ Y8的截距 | ||
| + | Y9 0.034 0.046 0.741 0.458 !@ Y9的截距 | ||
| + | Y10 -0.016 0.062 -0.261 0.794 !@ Y10的截距 | ||
| + | Y11 0.010 0.047 0.202 0.840 !@ Y11的截距 | ||
| + | Y12 0.006 0.045 0.134 0.894 !@ Y12的截距 | ||
| + | |||
| + | Variances | ||
| + | F5 1.000 0.000 999.000 999.000 !@ F5的方差。999.000代表没有计算,也就是没有这个结果(下同) | ||
| + | |||
| + | Residual Variances !@ 残差,潜变量未能解释的方差 | ||
| + | Y1 0.348 0.043 8.132 0.000 !@ Y1的残差 | ||
| + | Y2 0.251 0.027 9.465 0.000 !@ Y2的残差 | ||
| + | Y3 0.320 0.026 12.271 0.000 !@ Y3的残差 | ||
| + | Y4 0.366 0.045 8.187 0.000 !@ Y4的残差 | ||
| + | Y5 0.268 0.026 10.303 0.000 !@ Y5的残差 | ||
| + | Y6 0.330 0.028 11.636 0.000 !@ Y6的残差 | ||
| + | Y7 0.272 0.038 7.094 0.000 !@ Y7的残差 | ||
| + | Y8 0.282 0.025 11.445 0.000 !@ Y8的残差 | ||
| + | Y9 0.276 0.024 11.416 0.000 !@ Y9的残差 | ||
| + | Y10 0.362 0.045 8.107 0.000 !@ Y10的残差 | ||
| + | Y11 0.266 0.027 9.854 0.000 !@ Y11的残差 | ||
| + | Y12 0.323 0.027 11.991 0.000 !@ Y12的残差 | ||
| + | F1 0.663 0.062 10.679 0.000 !@ F1的残差 | ||
| + | F2 0.714 0.057 12.629 0.000 !@ F2的残差 | ||
| + | F3 0.609 0.066 9.155 0.000 !@ F3的残差 | ||
| + | F4 0.782 0.050 15.527 0.000 !@ F4的残差 | ||
| + | |||
| + | |||
| + | R-SQUARE !@ R的平方,观察变量和潜变量被因子解释的百分比 | ||
| + | |||
| + | Observed Two-Tailed | ||
| + | Variable Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | Y1 0.798 0.027 29.932 0.000 !@ Y1被F1解释的百分比 | ||
| + | Y2 0.760 0.028 27.580 0.000 !@ Y2被F1解释的百分比 | ||
| + | Y3 0.658 0.030 21.641 0.000 !@ Y3被F1解释的百分比 | ||
| + | Y4 0.799 0.026 30.138 0.000 !@ Y4被F2解释的百分比 | ||
| + | Y5 0.736 0.028 26.256 0.000 !@ Y5被F2解释的百分比 | ||
| + | Y6 0.685 0.030 23.083 0.000 !@ Y6被F2解释的百分比 | ||
| + | Y7 0.856 0.022 39.504 0.000 !@ Y7被F3解释的百分比 | ||
| + | Y8 0.739 0.026 28.938 0.000 !@ Y8被F3解释的百分比 | ||
| + | Y9 0.737 0.026 28.588 0.000 !@ Y9被F3解释的百分比 | ||
| + | Y10 0.811 0.025 32.184 0.000 !@ Y10被F4解释的百分比 | ||
| + | Y11 0.762 0.026 28.815 0.000 !@ Y11被F4解释的百分比 | ||
| + | Y12 0.683 0.029 23.439 0.000 !@ Y12被F4解释的百分比 | ||
| + | |||
| + | Latent Two-Tailed | ||
| + | Variable Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性) | ||
| + | |||
| + | F1 0.337 0.062 5.425 0.000 !@ F1被F5解释的百分比 | ||
| + | F2 0.286 0.057 5.048 0.000 !@ F2被F5解释的百分比 | ||
| + | F3 0.391 0.066 5.889 0.000 !@ F3被F5解释的百分比 | ||
| + | F4 0.218 0.050 4.329 0.000 !@ F4被F5解释的百分比 | ||
| + | |||
| + | |||
| + | QUALITY OF NUMERICAL RESULTS | ||
| + | |||
| + | Condition Number for the Information Matrix 0.558E-02 !@ 信息矩阵的条件数 | ||
| + | (ratio of smallest to largest eigenvalue) | ||
| + | |||
| + | |||
| + | DIAGRAM INFORMATION !@ 图形信息 | ||
| + | |||
| + | Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram. !@ 在Diagram菜单下显示图形信息 | ||
| + | If running Mplus from the Mplus Diagrammer, the diagram opens automatically. !@ 如果是从Mplus Diagrammer运行Mplus,会自动显示图形信息 | ||
| + | |||
| + | Diagram output | ||
| + | c:\program files\mplus\mplus examples\user's guide examples\mptext1.dgm | ||
| + | |||
| + | Beginning Time: 13:53:30 !@ 命令语句(程序)开始运行时间 | ||
| + | Ending Time: 13:53:31 !@ 命令语句(程序)结束运行时间 | ||
| + | Elapsed Time: 00:00:01 !@ 程序运行花费时间</pre> | ||
2017年6月17日 (六) 16:42的最新版本
示意图
代码与注释
TITLE: this is an example of a second-order factor analysis ! 这是标题
DATA: FILE IS ex5.6.dat; ! 读数据文件
VARIABLE: NAMES ARE y1-y12; ! 数据文件中有12个变量,命名y1-y12
MODEL: f1 BY y1-y3; ! 定义第1个因素,该因素的测量指标有:y1,y2,y3。
f2 BY y4-y6; ! 定义第2个因素,该因素的测量指标有:y4,y5,y6。
f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。
f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。
f5 BY f1-f4; ! 二阶因素f5
OUTPUT:STANDARDIZED; ! 报告标准化之后的结果,这是增加的命令语句
结果
INPUT INSTRUCTIONS !@ 输入的命令语句,会全部显示,下面几行就是输入的命令语句
TITLE: this is an example of a second-order factor analysis ! 这是标题
DATA: FILE IS ex5.6.dat; ! 读数据文件,文件名要正确,文件路径与对应的分析程序在同一目录;或标明绝对路径,比如:c:\mplus\ex5.6.dat。
VARIABLE: NAMES ARE y1-y12; ! 读取数据,该数据文件中包括12个变量的数据,变量名称可以自己。比如,可以是y1-y12,也可以是item1-item12。
MODEL: f1 BY y1-y3; ! 定义第1个因素,该因素的测量指标有:y1,y2,y3。如果上面为item1-item6,则修改为item1-item3
f2 BY y4-y6; ! 定义第2个因素,该因素的测量指标有:y4,y5,y6。
f3 BY y7-y9; ! 定义第3个因素,该因素的测量指标有:y7,y8,y9。
f4 BY y10-y12; ! 定义第4个因素,该因素的测量指标有:y10,y11,y12。
f5 BY f1-f4; ! 定义第5个因素,该因素的测量指标有:f1,f2,f3,f4。
OUTPUT:STANDARDIZED; ! 报告标准化之后的结果,这是增加的命令语句。
INPUT READING TERMINATED NORMALLY !@ 数据读取正常
this is an example of a second-order factor analysis !@ TITLE,标题
SUMMARY OF ANALYSIS !@分析总体情况
Number of groups 1 !@ 1组数据,也就是样本没有分组
Number of observations 500 !@ 样本量500
Number of dependent variables 12 !@ (因)变量12个
Number of independent variables 0 !@ (自)变量0个
Number of continuous latent variables 5 !@ 潜变量5个
Observed dependent variables !@ 观测(因)变量
Continuous !@ 观测(因)变量为连续变量 Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9 Y10 Y11 Y12
Y1 Y2 Y3 Y4 Y5 Y6
Y7 Y8 Y9 Y10 Y11 Y12
Continuous latent variables !@ 潜变量 F1 F2 F3 F4 F5
F1 F2 F3 F4 F5
Estimator ML !@ 估计方法:最大似然法
Information matrix OBSERVED !@ 信息矩阵:观测数据
Maximum number of iterations 1000 !@ 最大迭代次数1000次
Convergence criterion 0.500D-04 !@ 聚合标准(或翻译为收敛标准)
Maximum number of steepest descent iterations 20 !@ 迭代下降最大数:20
Input data file(s) !@ 输入文件:ex5.6.dat
ex5.6.dat
Input data format FREE !@ 输入文件格式:自由格式,这是Mplus的默认格式
THE MODEL ESTIMATION TERMINATED NORMALLY !@ 模型估计正常终止,如果是非正常终止,就需要检查数据或命令语
MODEL FIT INFORMATION !@ 模型拟合指数
Number of Free Parameters 40 !@ 自由参数的个数:40个
Loglikelihood !@ 似然函数值的自然对数
H0 Value -7211.373
H1 Value -7188.001
Information Criteria !@ 信息标准
Akaike (AIC) 14502.746 !@ AIC
Bayesian (BIC) 14671.330 !@ BIC
Sample-Size Adjusted BIC 14544.368 !@ 考虑样本量,调整后的BIC值
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit !@ 卡方检验的结果
Value 46.743 !@ 卡方值
Degrees of Freedom 50 !@ 自由度
P-Value 0.6049 !@ 显著性
RMSEA (Root Mean Square Error Of Approximation) !@ RMSEA的结果
Estimate 0.000 !@ RMSEA的值
90 Percent C.I. 0.000 0.026 !@ RMSEA的90%置信区间
Probability RMSEA <= .05 1.000
CFI/TLI !@ CFI/TFI的结果
CFI 1.000 !@ CFI的结果
TLI 1.001 !@ TLI的结果
Chi-Square Test of Model Fit for the Baseline Model !@ 基准模型(基线模型)的卡方检验结果
Value 4012.035 !@ 卡方值
Degrees of Freedom 66 !@ 自由度
P-Value 0.0000 !@ 显著性
SRMR (Standardized Root Mean Square Residual) !@ SRMR的结果
Value 0.019
MODEL RESULTS !@ 模型结果,非标准化的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 BY
Y1 1.000 0.000 999.000 999.000 !@ Y1的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
Y2 0.760 0.031 24.275 0.000 !@ Y2的非标准化因子负荷
Y3 0.669 0.030 22.309 0.000 !@ Y3的非标准化因子负荷
F2 BY
Y4 1.000 0.000 999.000 999.000 !@ Y4的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
Y5 0.718 0.030 23.976 0.000 !@ Y5的非标准化因子负荷
Y6 0.703 0.031 22.853 0.000 !@ Y6的非标准化因子负荷
F3 BY
Y7 1.000 0.000 999.000 999.000 !@ Y7的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
Y8 0.702 0.026 26.955 0.000 !@ Y8的非标准化因子负荷
Y9 0.691 0.026 26.764 0.000 !@ Y9的非标准化因子负荷
F4 BY
Y10 1.000 0.000 999.000 999.000 !@ Y10的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
Y11 0.742 0.029 25.350 0.000 !@ Y11的非标准化因子负荷
Y12 0.669 0.029 23.461 0.000 !@ Y12的非标准化因子负荷
F5 BY
F1 1.000 0.000 999.000 999.000 !@ F1的非标准化因子负荷,999.000代表没有计算,也就是没有这个结果(下同)
F2 0.944 0.148 6.397 0.000 !@ F2的非标准化因子负荷
F3 1.168 0.179 6.516 0.000 !@ F3的非标准化因子负荷
F4 0.854 0.139 6.142 0.000 !@ F4的非标准化因子负荷
Intercepts !@ 截距,潜变量为0时,观察变量的值
Y1 0.011 0.059 0.183 0.855 !@ Y1的截距
Y2 0.028 0.046 0.617 0.537 !@ Y2的截距
Y3 0.005 0.043 0.109 0.913 !@ Y3的截距
Y4 0.100 0.060 1.652 0.099 !@ Y4的截距
Y5 0.078 0.045 1.730 0.084 !@ Y5的截距
Y6 0.076 0.046 1.671 0.095 !@ Y6的截距
Y7 0.024 0.061 0.390 0.697 !@ Y7的截距
Y8 0.025 0.046 0.545 0.585 !@ Y8的截距
Y9 0.034 0.046 0.741 0.458 !@ Y9的截距
Y10 -0.016 0.062 -0.261 0.794 !@ Y10的截距
Y11 0.010 0.047 0.202 0.840 !@ Y11的截距
Y12 0.006 0.045 0.134 0.894 !@ Y12的截距
Variances !@ 因子方差
F5 0.464 0.100 4.657 0.000 !@ F5的方差
Residual Variances !@ 残差,潜变量未能解释的方差
Y1 0.348 0.043 8.132 0.000 !@ Y1的残差
Y2 0.251 0.027 9.465 0.000 !@ Y2的残差
Y3 0.320 0.026 12.271 0.000 !@ Y3的残差
Y4 0.366 0.045 8.187 0.000 !@ Y4的残差
Y5 0.268 0.026 10.303 0.000 !@ Y5的残差
Y6 0.330 0.028 11.636 0.000 !@ Y6的残差
Y7 0.272 0.038 7.094 0.000 !@ Y7的残差
Y8 0.282 0.025 11.445 0.000 !@ Y8的残差
Y9 0.276 0.024 11.416 0.000 !@ Y9的残差
Y10 0.362 0.045 8.107 0.000 !@ Y10的残差
Y11 0.266 0.027 9.854 0.000 !@ Y11的残差
Y12 0.323 0.027 11.991 0.000 !@ Y12的残差
F1 0.913 0.103 8.855 0.000 !@ F1的残差
F2 1.036 0.107 9.672 0.000 !@ F2的残差
F3 0.984 0.119 8.237 0.000 !@ F3的残差
F4 1.213 0.115 10.567 0.000 !@ F4的残差
STANDARDIZED MODEL RESULTS !@ 模型结果,标准化的结果
STDYX Standardization !@ 观测变量、潜变量均标准化后的结果,也就是全部标准化后的结果。一般报告这个结果。
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 BY
Y1 0.894 0.015 59.864 0.000 !@ Y1的标准化因子负荷
Y2 0.872 0.016 55.160 0.000 !@ Y2的标准化因子负荷
Y3 0.811 0.019 43.281 0.000 !@ Y3的标准化因子负荷
F2 BY
Y4 0.894 0.015 60.275 0.000 !@ Y4的标准化因子负荷
Y5 0.858 0.016 52.512 0.000 !@ Y5的标准化因子负荷
Y6 0.828 0.018 46.167 0.000 !@ Y6的标准化因子负荷
F3 BY
Y7 0.925 0.012 79.008 0.000 !@ Y7的标准化因子负荷
Y8 0.859 0.015 57.876 0.000 !@ Y8的标准化因子负荷
Y9 0.858 0.015 57.175 0.000 !@ Y9的标准化因子负荷
F4 BY
Y10 0.900 0.014 64.368 0.000 !@ Y10的标准化因子负荷
Y11 0.873 0.015 57.629 0.000 !@ Y11的标准化因子负荷
Y12 0.826 0.018 46.877 0.000 !@ Y12的标准化因子负荷
F5 BY
F1 0.580 0.053 10.851 0.000 !@ F1的标准化因子负荷
F2 0.534 0.053 10.096 0.000 !@ F2的标准化因子负荷
F3 0.626 0.053 11.779 0.000 !@ F3的标准化因子负荷
F4 0.467 0.054 8.658 0.000 !@ F4的标准化因子负荷
Intercepts !@ 截距,潜变量为0时,观察变量的值
Y1 0.008 0.045 0.183 0.855 !@ Y1的截距
Y2 0.028 0.045 0.617 0.537 !@ Y2的截距
Y3 0.005 0.045 0.109 0.913 !@ Y3的截距
Y4 0.074 0.045 1.650 0.099 !@ Y4的截距
Y5 0.077 0.045 1.728 0.084 !@ Y5的截距
Y6 0.075 0.045 1.668 0.095 !@ Y6的截距
Y7 0.017 0.045 0.390 0.697 !@ Y7的截距
Y8 0.024 0.045 0.545 0.585 !@ Y8的截距
Y9 0.033 0.045 0.741 0.459 !@ Y9的截距
Y10 -0.012 0.045 -0.261 0.794 !@ Y10的截距
Y11 0.009 0.045 0.202 0.840 !@ Y11的截距
Y12 0.006 0.045 0.134 0.894 !@ Y12的截距
Variances !@ 因子方差
F5 1.000 0.000 999.000 999.000 !@ F5的方差。999.000代表没有计算,也就是没有这个结果(下同)
Residual Variances !@ 残差,潜变量未能解释的方差
Y1 0.202 0.027 7.557 0.000 !@ Y1的残差
Y2 0.240 0.028 8.689 0.000 !@ Y2的残差
Y3 0.342 0.030 11.247 0.000 !@ Y3的残差
Y4 0.201 0.026 7.601 0.000 !@ Y4的残差
Y5 0.264 0.028 9.403 0.000 !@ Y5的残差
Y6 0.315 0.030 10.621 0.000 !@ Y6的残差
Y7 0.144 0.022 6.634 0.000 !@ Y7的残差
Y8 0.261 0.026 10.236 0.000 !@ Y8的残差
Y9 0.263 0.026 10.225 0.000 !@ Y9的残差
Y10 0.189 0.025 7.516 0.000 !@ Y10的残差
Y11 0.238 0.026 8.981 0.000 !@ Y11的残差
Y12 0.317 0.029 10.901 0.000 !@ Y12的残差
F1 0.663 0.062 10.679 0.000 !@ F1的残差
F2 0.714 0.057 12.629 0.000 !@ F2的残差
F3 0.609 0.066 9.155 0.000 !@ F3的残差
F4 0.782 0.050 15.527 0.000 !@ F4的残差
STDY Standardization !@ 观测变量标准化后的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 BY
Y1 0.894 0.015 59.864 0.000 !@ Y1的标准化因子负荷
Y2 0.872 0.016 55.160 0.000 !@ Y2的标准化因子负荷
Y3 0.811 0.019 43.281 0.000 !@ Y3的标准化因子负荷
F2 BY
Y4 0.894 0.015 60.275 0.000 !@ Y4的标准化因子负荷
Y5 0.858 0.016 52.512 0.000 !@ Y5的标准化因子负荷
Y6 0.828 0.018 46.167 0.000 !@ Y6的标准化因子负荷
F3 BY
Y7 0.925 0.012 79.008 0.000 !@ Y7的标准化因子负荷
Y8 0.859 0.015 57.876 0.000 !@ Y8的标准化因子负荷
Y9 0.858 0.015 57.175 0.000 !@ Y9的标准化因子负荷
F4 BY
Y10 0.900 0.014 64.368 0.000 !@ Y10的标准化因子负荷
Y11 0.873 0.015 57.629 0.000 !@ Y11的标准化因子负荷
Y12 0.826 0.018 46.877 0.000 !@ Y12的标准化因子负荷
F5 BY
F1 0.580 0.053 10.851 0.000 !@ F1的标准化因子负荷
F2 0.534 0.053 10.096 0.000 !@ F2的标准化因子负荷
F3 0.626 0.053 11.779 0.000 !@ F3的标准化因子负荷
F4 0.467 0.054 8.658 0.000 !@ F4的标准化因子负荷
Intercepts !@ 截距,潜变量为0时,观察变量的值
Y1 0.008 0.045 0.183 0.855 !@ Y1的截距
Y2 0.028 0.045 0.617 0.537 !@ Y2的截距
Y3 0.005 0.045 0.109 0.913 !@ Y3的截距
Y4 0.074 0.045 1.650 0.099 !@ Y4的截距
Y5 0.077 0.045 1.728 0.084 !@ Y5的截距
Y6 0.075 0.045 1.668 0.095 !@ Y6的截距
Y7 0.017 0.045 0.390 0.697 !@ Y7的截距
Y8 0.024 0.045 0.545 0.585 !@ Y8的截距
Y9 0.033 0.045 0.741 0.459 !@ Y9的截距
Y10 -0.012 0.045 -0.261 0.794 !@ Y10的截距
Y11 0.009 0.045 0.202 0.840 !@ Y11的截距
Y12 0.006 0.045 0.134 0.894 !@ Y12的截距
Variances
F5 1.000 0.000 999.000 999.000 !@ F5的方差。999.000代表没有计算,也就是没有这个结果(下同)
Residual Variances !@ 残差,潜变量未能解释的方差
Y1 0.202 0.027 7.557 0.000 !@ Y1的残差
Y2 0.240 0.028 8.689 0.000 !@ Y2的残差
Y3 0.342 0.030 11.247 0.000 !@ Y3的残差
Y4 0.201 0.026 7.601 0.000 !@ Y4的残差
Y5 0.264 0.028 9.403 0.000 !@ Y5的残差
Y6 0.315 0.030 10.621 0.000 !@ Y6的残差
Y7 0.144 0.022 6.634 0.000 !@ Y7的残差
Y8 0.261 0.026 10.236 0.000 !@ Y8的残差
Y9 0.263 0.026 10.225 0.000 !@ Y9的残差
Y10 0.189 0.025 7.516 0.000 !@ Y10的残差
Y11 0.238 0.026 8.981 0.000 !@ Y11的残差
Y12 0.317 0.029 10.901 0.000 !@ Y12的残差
F1 0.663 0.062 10.679 0.000 !@ F1的残差
F2 0.714 0.057 12.629 0.000 !@ F2的残差
F3 0.609 0.066 9.155 0.000 !@ F3的残差
F4 0.782 0.050 15.527 0.000 !@ F4的残差
STD Standardization !@ 潜变量标准化后的结果
Two-Tailed
Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 BY
Y1 1.174 0.048 24.382 0.000 !@ Y1的非标准化因子负荷
Y2 0.892 0.038 23.520 0.000 !@ Y2的非标准化因子负荷
Y3 0.785 0.037 21.235 0.000 !@ Y3的非标准化因子负荷
F2 BY
Y4 1.204 0.049 24.412 0.000 !@ Y4的非标准化因子负荷
Y5 0.864 0.038 23.002 0.000 !@ Y5的非标准化因子负荷
Y6 0.847 0.039 21.825 0.000 !@ Y6的非标准化因子负荷
F3 BY
Y7 1.272 0.048 26.282 0.000 !@ Y7的非标准化因子负荷
Y8 0.893 0.038 23.433 0.000 !@ Y8的非标准化因子负荷
Y9 0.879 0.038 23.359 0.000 !@ Y9的非标准化因子负荷
F4 BY
Y10 1.245 0.050 24.845 0.000 !@ Y10的非标准化因子负荷
Y11 0.924 0.039 23.727 0.000 !@ Y11的非标准化因子负荷
Y12 0.834 0.038 21.875 0.000 !@ Y12的非标准化因子负荷
X
F5 BY
F1 0.580 0.053 10.851 0.000 !@ F1的非标准化因子负荷
F2 0.534 0.053 10.096 0.000 !@ F2的非标准化因子负荷
F3 0.626 0.053 11.779 0.000 !@ F3的非标准化因子负荷
F4 0.467 0.054 8.658 0.000 !@ F4的非标准化因子负荷
Intercepts !@ 截距,潜变量为0时,观察变量的值
Y1 0.011 0.059 0.183 0.855 !@ Y1的截距
Y2 0.028 0.046 0.617 0.537 !@ Y2的截距
Y3 0.005 0.043 0.109 0.913 !@ Y3的截距
Y4 0.100 0.060 1.652 0.099 !@ Y4的截距
Y5 0.078 0.045 1.730 0.084 !@ Y5的截距
Y6 0.076 0.046 1.671 0.095 !@ Y6的截距
Y7 0.024 0.061 0.390 0.697 !@ Y7的截距
Y8 0.025 0.046 0.545 0.585 !@ Y8的截距
Y9 0.034 0.046 0.741 0.458 !@ Y9的截距
Y10 -0.016 0.062 -0.261 0.794 !@ Y10的截距
Y11 0.010 0.047 0.202 0.840 !@ Y11的截距
Y12 0.006 0.045 0.134 0.894 !@ Y12的截距
Variances
F5 1.000 0.000 999.000 999.000 !@ F5的方差。999.000代表没有计算,也就是没有这个结果(下同)
Residual Variances !@ 残差,潜变量未能解释的方差
Y1 0.348 0.043 8.132 0.000 !@ Y1的残差
Y2 0.251 0.027 9.465 0.000 !@ Y2的残差
Y3 0.320 0.026 12.271 0.000 !@ Y3的残差
Y4 0.366 0.045 8.187 0.000 !@ Y4的残差
Y5 0.268 0.026 10.303 0.000 !@ Y5的残差
Y6 0.330 0.028 11.636 0.000 !@ Y6的残差
Y7 0.272 0.038 7.094 0.000 !@ Y7的残差
Y8 0.282 0.025 11.445 0.000 !@ Y8的残差
Y9 0.276 0.024 11.416 0.000 !@ Y9的残差
Y10 0.362 0.045 8.107 0.000 !@ Y10的残差
Y11 0.266 0.027 9.854 0.000 !@ Y11的残差
Y12 0.323 0.027 11.991 0.000 !@ Y12的残差
F1 0.663 0.062 10.679 0.000 !@ F1的残差
F2 0.714 0.057 12.629 0.000 !@ F2的残差
F3 0.609 0.066 9.155 0.000 !@ F3的残差
F4 0.782 0.050 15.527 0.000 !@ F4的残差
R-SQUARE !@ R的平方,观察变量和潜变量被因子解释的百分比
Observed Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
Y1 0.798 0.027 29.932 0.000 !@ Y1被F1解释的百分比
Y2 0.760 0.028 27.580 0.000 !@ Y2被F1解释的百分比
Y3 0.658 0.030 21.641 0.000 !@ Y3被F1解释的百分比
Y4 0.799 0.026 30.138 0.000 !@ Y4被F2解释的百分比
Y5 0.736 0.028 26.256 0.000 !@ Y5被F2解释的百分比
Y6 0.685 0.030 23.083 0.000 !@ Y6被F2解释的百分比
Y7 0.856 0.022 39.504 0.000 !@ Y7被F3解释的百分比
Y8 0.739 0.026 28.938 0.000 !@ Y8被F3解释的百分比
Y9 0.737 0.026 28.588 0.000 !@ Y9被F3解释的百分比
Y10 0.811 0.025 32.184 0.000 !@ Y10被F4解释的百分比
Y11 0.762 0.026 28.815 0.000 !@ Y11被F4解释的百分比
Y12 0.683 0.029 23.439 0.000 !@ Y12被F4解释的百分比
Latent Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value !@ 估计值 标准误 估计标准误 P值(显著性)
F1 0.337 0.062 5.425 0.000 !@ F1被F5解释的百分比
F2 0.286 0.057 5.048 0.000 !@ F2被F5解释的百分比
F3 0.391 0.066 5.889 0.000 !@ F3被F5解释的百分比
F4 0.218 0.050 4.329 0.000 !@ F4被F5解释的百分比
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.558E-02 !@ 信息矩阵的条件数
(ratio of smallest to largest eigenvalue)
DIAGRAM INFORMATION !@ 图形信息
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram. !@ 在Diagram菜单下显示图形信息
If running Mplus from the Mplus Diagrammer, the diagram opens automatically. !@ 如果是从Mplus Diagrammer运行Mplus,会自动显示图形信息
Diagram output
c:\program files\mplus\mplus examples\user's guide examples\mptext1.dgm
Beginning Time: 13:53:30 !@ 命令语句(程序)开始运行时间
Ending Time: 13:53:31 !@ 命令语句(程序)结束运行时间
Elapsed Time: 00:00:01 !@ 程序运行花费时间